FATE v2.0 Documentation
05/25/2024
Table of contents
- Introduction
- Air quality methods
- Perturbing emissions
- Health impact assessment methods
- VSL calculation
Introduction
The Fast Assessment of Transportation Emissions (FATE) model evaluates air quality and health impacts associated with present or future changes in air pollutant emissions from 9 sectors, including 4 transportation sub-sectors. The tool estimates the national population-weighted ambient PM2.5 exposure (annual average in µg/m3) for 165 countries and ozone (O3) exposure (6-month average of the 8h daily maximum O3 in ppb) for 19 individual G20 countries and 24 additional EU member countries. It also outputs the number of premature deaths and years of life lost (YLL) associated with exposure to these two pollutants by country, disease, and age group. Health outputs of the tool include 5th and 95th percentile estimates that reflect uncertainty in the concentration-response relationship. FATE also optionally quantifies the number of premature deaths to a dollar amount using the Value of a Statistical Life (VSL) using two methods.
FATE is a reduced-complexity air quality model, allowing users to simulate national, regional, or global scenarios without the high computational costs usually required by chemical transport models. The extent to which exposures of PM2.5 and O3 respond to changes in emissions of primary pollutant species, denoted as sensitivities, are calculated using the adjoint of the GEOS-Chem model. The health impacts associated with exposure to these pollutants are calculated using methods consistent with the Global Burden of Disease (GBD) 2019. To estimate health impacts in future years, the tool considers changes in pollutant exposure, projected changes in population, age distributions, and baseline disease rates at the national level.
Users can input absolute (tonnes, kt, or kg/m2) or relative (fractional) changes to FATE’s baseline emissions. These emissions can be specified either at the country scale, where gridding algorithms are applied using built-in country masks, or in user-specified grid cells. Users have the choice of using the GEOS-Chem global 2° × 2.5° resolution or the 0.1° × 0.1° resolution of the country mask grid for defining the gridded input option, though all gridded inputs are regridded to the coarser resolution in the model for the exposure module. Emissions can be perturbed for any year between 2015 and 2050. If users are confident that their emissions accurately represent total-sector emissions, they have an option to replace the FATE baseline for specific species, sectors, countries, grid cells, and years using the independent emissions input option. Users can also skip the exposure calculation and utilize only FATE’s health impacts module by providing independently modeled population-weighted exposure values at a national level. The tool provides the flexibility to run multiple scenarios and provide an alternative baseline.
Acknowledgments
FATE was first developed in 2021 by Caleb Braun, Erik Pronk, Arijit Sen, Claire Buysse, and Josh Miller. Jonathan Benoit, Gabe Hillman Alvarez, Arijit Sen, Josh Miller, Patricia Ferrini Rodrigues, and Lingzhi Jin developed versions 1.0 (2023) and 2.0 (2024).
Baseline Emissions
Baseline emissions projections used in FATE are derived primarily from the ECLIPSE v6b Reference scenario. ECLIPSE classifies total annual emissions into 7 primary pollutant species and 9 source sectors at a grid resolution of 0.5° × 0.5°. FATE regrids ECLIPSE emissions to a 0.1° × 0.1° grid during preprocessing to match the resolution of FATE’s country mask. ECLIPSE v6b baseline emissions data are defined for the years 2015, 2020, 2025, 2030, 2040, and 2050, while values for intermediate years are interpolated linearly by grid cell. Emissions projections for the agriculture, waste, energy, industry, residential, and shipping sectors come directly from ECLIPSE v6b. Country totals for on-road transportation emissions projections are scaled annually from 2020 to 2050 to match national totals modeled for ICCT’s Global Health Study baseline scenario using ICCT’s Roadmap model. Where ECLIPSE v6b lacks detailed transportation emissions, the spatial distribution from ECLIPSE v5a or other transport subsectors is used for the scaling. Non-shipping transportation emissions are separated into on-road diesel, on-road gasoline, and other transport. FATE is intended for use in policy contexts, so secondary pollutant exposure from natural emission sources remains constant across time.
Sectors
ECLIPSE data classifies emissions based on their sources, breaking down each primary pollutant species by sector. The sectors, including four specific to transportation, are listed in the table below. On-road transport is encompassed by diesel and gasoline sectors (TRA_MD, and TRA_GSL), while the shipping sector (SHP) represents emissions from maritime shipping. The other transportation sector (TRA_OTH) includes take-off and landing emissions from aviation and other forms of off-road transport. Upstream emissions associated with one sector but produced by another sector are considered within the emissions of the sector that directly produces those emissions. For instance, the emissions from electricity generation used to power electric vehicles are accounted for in the energy sector’s emissions, not in the transportation sector’s.
| Abbreviation | Description |
|---|---|
| WST | Waste |
| AGR | Agriculture (NH3 only) plus waste burning on fields |
| ENE | Power plants, energy conversion, and extraction |
| IND | Industry (combustion and processing) plus solvents (VOCs only) |
| RES | Residential and commercial |
| FLR | Upstream production field flaring or venting |
| SHP | Maritime shipping |
| TRA_GSL | Road transport gasoline (+ other non-diesel fuels) |
| TRA_MD | Road transport diesel |
| TRA_OTH | Other non-road transport (but excluding all maritime shipping) |
FATE’s exposure module has been calibrated to most accurately model the impact of changes in the on-road sectors and related upstream well-to-tank emissions during fuel production from the energy and industry sectors. Users are advised against using FATE’s exposure module for any sector when emission perturbations are significantly larger than the on-road emissions baseline, at altitude, or over large bodies of water. It is recommended to provide an independently modeled population-weighted exposure estimate when working with these out-of-scope emission perturbations.
Species
FATE quantifies health burden by assessing a population’s exposure to PM2.5 and O3, which are secondary pollutants formed in the atmosphere from primary emissions by vehicles and other sources. While certain sectors directly emit PM2.5, it is generally understood that the contribution from primary emissions within the transportation sectors is relatively small compared to secondary production, so only secondary PM2.5 is considered in FATE. See the table at the end of this section for the full set of primary species modeled.
PM2.5 refers to fine particulate matter with a diameter of 2.5 micrometers or smaller. As PM2.5 encompasses particles of various molecular compositions, its production can originate from diverse sources. Primary black carbon (BC) and organic carbon (OC) contribute to the formation of secondary organic aerosols (SOA), which are a significant component of PM2.5. Additionally, ammonia (NH3) reacts with sulfur dioxide (SO2) and nitrogen oxides (NOx) to generate ammonium sulfate (NH4HSO4) and ammonium nitrate (NH4NO3) particles, further contributing to the concentration of PM2.5. In FATE, BC, OC, NH3, NOx, and SO2 are considered precursor species in the production of PM2.5.
Ozone (O3) is formed through photochemical reactions involving NOx and volatile organic compounds (VOCs). Carbon monoxide (CO) indirectly influences the production of these secondary pollutants through its participation in atmospheric reactions. In FATE, NOx, VOC, and CO are considered precursor species in the production of O3.
O3 exposure is sensitive to volatile organic compounds (VOCs); however, there are only a few species of VOCs that are considered in GEOS-Chem. For more accurate VOC scenarios, we suggest that users only consider emissions of the following species: ≥C4-alkanes, formaldehyde (HCHO), ethane (C2H6), propane (C3H8), propene (C3H6), acetone, methyl ethyl ketone and acetaldehyde.
| Abbreviation | Chemical species | Emitted species | Secondary pollutants |
|---|---|---|---|
| BC | Primary black carbon | Carbon (C) | PM2.5 |
| OC | Primary organic carbon | Carbon (C) | PM2.5. |
| NH3 | Ammonia | Ammonia (NH3) | PM2.5 |
| SO2 | Sulfur dioxide | Sulfur dioxide (SO2) | PM2.5 |
| NOx | Nitrogen oxides | Nitrogen (N) | PM2.5, O3 |
| CO | Carbon monoxide | Carbon monoxide (CO) | O3 |
| VOC | Non-methane volatile organic compounds | ≥C4-alkanes, formaldehyde (HCHO), ethane (C2H6), propane (C3H8), propene (C3H6), acetone, methyl ethyl ketone and acetaldehyde (all units are C) | O3 |
Air quality methods
FATE utilizes sensitivities derived from the adjoint of the GEOS-Chem model to estimate national population-weighted concentrations of PM2.5 and O3. The adjoint of the GEOS-Chem model identifies the emission sources that contribute to exposure by calculating the sensitivity of a nation’s population-weighted pollutant exposure (PM2.5 or O3) to an emissions perturbation in any of the global model’s 2° × 2.5° grid cells. The adjoint sensitivities are calculated for each chemical species, thus they do not vary by sector. These coefficients are provided as 2D arrays for surface-layer emissions, as shown in Figure 1.
The adjoint sensitivities approximate a relationship that is complex and non-linear: it depends on atmospheric transport, chemical speciation, and population distribution, which all vary across a global 2-dimensional grid. FATE represents a linear approximation of this relationship around the scale of emissions changes expected from transportation mitigation policies. As a result, FATE’s exposure module will most accurately model changes in emissions from transportation policy scenarios for the same year. The expected scale of emissions changes across decades from all sectors is much larger than that expected from transport-sector interventions, so the assumption of linearity does not hold well. FATE will produce greater inaccuracies when modeling large exposure changes and should be framed primarily in a policy context to understand the impact of different transport interventions in a given year.
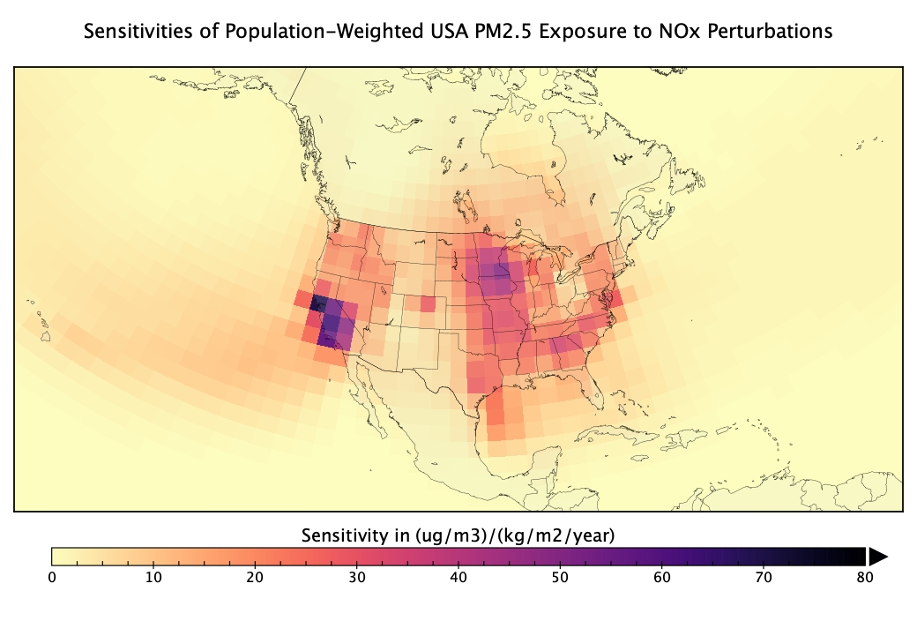
Figure 1. Subset of USA PM2.5 adjoint sensitivities for NOx emissions. Values represent the degree to which grid cells are sources of NOx that contribute to population-weighted PM2.5 exposure in the United States.
Utilizing these coefficients simplifies the population-weighted exposure calculation in FATE, reducing it to a single multiplication:
\[Exposure = Adjoint\ Sensitivities \times Perturbed\ Emissions\]The perturbed emissions are re-gridded to match the 2° × 2.5° resolution of the adjoint sensitives and multiplied element-wise. This calculation results in a gridded product at 2° × 2.5° resolution, which is then aggregated to the national level for rescaling and health impacts assessment. Note that FATE cannot produce gridded concentrations because the gridded intermediary represents exposure sources for a given country without details on the role of population distribution or how exposure may vary within a country.
PM2.5 coefficients give the sensitivity to emissions of BC, OC, NH3, NOx, and SO2 for 165 countries (Figure 2). O3 sensitivities approximate the impacts of NOx, CO, and VOC emissions on the maximum 6-month mean of the daily 8-hour maximum (MDA8) O3 for 43 countries (Figure 3). If users prefer to study MDA1 O3, FATE includes country-specific conversion factors from MDA8 to MDA1 O3 based on GEOS-Chem modeling results.
Figure 2. Countries with PM2.5 sensitivities. 165 countries are supported.
Figure 3. Countries with O3 sensitivities. 19 individual G20 countries and 24 additional EU member countries are supported.
Exposure Rescaling
Two rescaling factors are optionally applied to align exposure in FATE to GEOS-Chem exposure results from ICCT’s Global Health Study for on-road transportation: an adjustment to match absolute exposure values from the Global Health Study’s baseline in 2020 and an adjustment to avoided exposure with respect to the baseline scenario. These rescaling factors assume that FATE’s biases with respect to the Global Health Study GEOS-Chem results are evenly distributed across sources and within the spatial domain of countries. The same rescaling methods are applied to both secondary pollutant species.
The national population-weighted PM2.5 annual average concentrations (i.e., exposures) from the Global Health Study are calculated using satellite-derived estimates of surface PM2.5 concentrations in 2020 at the 0.1° × 0.1° scale applied as downscaling factors to the GEOS-Chem model’s PM2.5 concentrations at the 2° × 2.5° resolution. Using the fine-scale concentrations of the satellite-derived products improves the estimation of population exposure without changing the overall modeled value of PM2.5 concentrations at the coarse scale. Gridded concentrations are aggregated to a population-weighted average exposure by country for rescaling. Ozone concentrations include no adjustment to real-world measurements because no trusted ozone satellite products exist.
Absolute Exposure Rescaling
There are appreciable differences between GEOS-Chem simulated PM2.5 and O3 population-weighted exposure and the approximation using FATE’s sensitivities, so we also include an option to adjust (“rescale”) the absolute PM2.5 and O3 exposure to match those from the Global Health Study, which represents the most comprehensive GEOS-Chem modeling for transportation interventions. For the modeled year closest to 2020 in the specified baseline scenario, total exposure values are rescaled to match the 2020 population-weighted exposure from the Global Health Study. The relative scaling factor of unadjusted FATE exposures to GEOS-Chem exposures is applied to all other years and scenarios. Note that these total exposure rescaling factors are calculated live on the model, are applied separately by country and pollutant, and depend on the user’s baseline scenario. Total exposure rescaling ensures that absolute exposure values in a user’s baseline are consistent with published values in the Global Health Study independent of the completeness of a user’s emissions inventory.
Avoided Exposure Rescaling
An additional set of exposure rescaling factors is applied to exposure differences from the baseline scenario to calibrate the adjoint sensitivities to the scale of exposure changes expected from on-road emissions mitigation policies. The avoided exposure in the Global Health Study’s “All Measures Zero Grid” (ALLZG) scenario compared to the baseline scenario represents the scale of exposure changes expected from on-road transportation mitigation policies, including the maximum extent of reductions to grid emissions. When using the same emissions inputs and absolute exposure rescaling, FATE’s ALLZG-to-baseline avoided exposure differs from that of GEOS-Chem because the adjoint sensitivities were derived from out-of-date modeling results. The relative ratio of the GEOS-Chem avoided exposure to FATE’s defines avoided exposure rescaling factors. These factors are multiplied by avoided exposure from the user-defined baseline in FATE, are constant for all model runs, and can be considered a calibration of the adjoint sensitivities to the latest GEOS-Chem results.
Perturbing emissions
In FATE, the baseline emissions come from ECLIPSE v6b Reference scenario for 2015, 2020, 2025, 2030, 2040, and 2050 (interpolated annually), combined with annual on-road emissions from Roadmap. Users can perturb these baseline emissions for specific sectors, precursor species, years, countries (tabular input), and grid cells (gridded input).
To perturb emissions for an entire country, users specify a tabular input as a CSV file containing the desired emissions perturbations for different sectors, species, and years. FATE distributes this perturbation over ECLIPSE’s 0.1° × 0.1° grid by filling cells corresponding to the specified ISO with the specified perturbation using the internal country mask. In cases where multiple countries occupy a single grid cell, FATE applies border weighting to reduce the perturbation according to the fraction of the grid cell area occupied by the specified country. Note that tabular inputs only perturb emissions over land.
In place of inputting a perturbation for an entire country, users can specify a gridded perturbation as a netCDF file with a perturbation variable defined for sector, species, year, latitude, and longitude dimensions. This approach does not rely on FATE’s country mask and allows the user to specify perturbations for subregions. Users can specify a gridded perturbation at the 0.1° × 0.1° resolution of ECLIPSE or the 2° × 2.5° resolution of the adjoint sensitivities.
A gridded emissions perturbation adjusts the baseline emissions for the corresponding sectors, species, and years by grid cells. FATE then re-grids the perturbed emissions to the 2° × 2.5° grid (if necessary), performs element-wise multiplication with the adjoint sensitivities, and aggregates to population-weighted PM2.5 or O3 exposure by country. This population-weighted exposure is optionally rescaled as described above, then used in the impacts module to calculate the health burden associated with the perturbed emissions.
Users have three options for specifying how FATE should interpret the values of these perturbations: relative perturbation, absolute perturbation, and independent emissions.
Relative Perturbation
The relative perturbation option enables users to simulate the effects of percentage changes to emissions. This option is particularly useful for exploring the potential benefits from reductions in specific sectors, species, or regions, without requiring absolute emission reduction estimates. Inputs are provided as relative fractions with a value of one representing no change from the ECLIPSE baseline.
To apply a relative perturbation, FATE multiplies user-specified relative fractions by corresponding baseline emissions for the specified species, sectors, and years using the gridding methods outlined above.
Absolute Perturbation
The absolute perturbation option models change from FATE’s baseline as an absolute quantity, specified in units of tonnes, kt, or \(kg/m^{2}\). This perturbation type is useful when the baseline scenario does not accurately represent total-sector emissions or when the user wants to focus on perturbations to a sub-sector.
To obtain an absolute perturbation input for FATE, users may subtract their baseline scenario emissions from each alternate scenario for corresponding ISOs, species, sectors, and years. Positive absolute perturbations increase emissions compared to the baseline, while negative perturbations reduce baseline emissions.
For an absolute perturbation specified using the tabular input option, FATE calculates an equivalent relative perturbation with respect to the FATE baseline. This conversion is done by adding the absolute perturbation to corresponding baseline emissions for specified ISOs, species, sectors, and years and dividing by the same corresponding ECLIPSE emissions. The model then applies the same gridding process as for a relative perturbation. Converting to a relative perturbation ensures that the perturbation is distributed appropriately based on the magnitude of the unperturbed emissions.
In the case of a gridded absolute perturbation, the ECLIPSE baseline is directly perturbed for specified species, sectors, and grid cells by adding the gridded absolute perturbation to the baseline without the need for a conversion to a relative perturbation.
Independent Emissions
The independent option allows users to replace a portion of FATE’s baseline with their own emissions, measured in tonnes, kt, or kg/m2. This option is useful when the user has confidence that their baseline case accurately represents total-sector emissions.
Similar to handling tabular absolute perturbations, tabular independent emissions are also converted to relative perturbations in FATE. This conversion involves dividing the independent emissions by FATE’s baseline emissions for specified ISOs, species, sectors, and years. The model then calculates gridded perturbed emissions and exposure using the same process as for relative and absolute cases.
For gridded independent emissions, the user’s input replaces the ECLIPSE baseline directly for specified species, sectors, and grid cells after necessary unit conversion or re-gridding.
Health impact assessment methods
The health impacts of PM2.5 and O3 exposure are calculated for each country using the “attributable fraction” approach. This approach is widely used by the GBD study, the World Health Organization, the U.S. Environmental Protection Agency, and throughout the peer-reviewed literature. For each scenario, FATE estimates the number of cases of various health endpoints by age group attributable to each pollutant.
Health impact methods are consistent with the GBD 2019 study, published in June 2020. GBD studies are broadly respected and increasingly used to inform public health decision-making around the world, at all geopolitical levels – international, national, and sub-national. Risk-outcome pairs are only included in the GBD after thorough review of the epidemiological, toxicology, and human and animal study evidence. The GBD is published annually and is updated over time to reflect the evolution of the state of the science, including in epidemiology and air pollution exposure science.
Consistent with the risk-outcome pairs in the GBD, FATE calculates cases of the following health outcomes associated with PM2.5:
-
stroke
-
ischemic heart disease
-
chronic obstructive pulmonary disease (COPD)
-
lower respiratory infection
-
lung cancer
-
diabetes mellitus type 2
For O3, only cases of COPD are considered.
The equation used to calculate the disease burden associated with PM2.5 and O3 concentrations is:
\[M_{a,i,h} = \text{Pop}_{i} \times \ \text{Popfrac}_{a,h} \times Y_{a,c,h} \times \left\lbrack \frac{\text{RR}_{a,i,h} - 1}{\text{RR}_{a,i,h}} \right\rbrack\]Where:
-
\(M\) is the disease burden (pollutant-attributable deaths or years of life lost) in geographic unit \(i\) for age group \(a\) and health endpoint \(h\)
-
\(\text{Pop}\) is the population in the geographic unit \(i\)
-
\(\text{Popfrac}\) is the population fraction for age group \(a\) and health endpoint \(h\)
-
\(Y\) is the baseline incidence rate (deaths or years of life lost per 100,000 people) in country \(c\) for age group \(a\) and health endpoint \(h\)
-
\(\text{RR}\) is relative risk in grid cell \(i\) for age group \(a\) and health endpoint \(h\)
The quantity in brackets is the population attributable fraction – the fraction of disease in a population that is attributable to the risk factor (in this case annual average PM2.5 or six-month average of 8-hour daily maximum O3).
A key feature of the PM2.5 concentration-response curves is that they are nonlinear and flatten considerably at high concentrations, particularly for cardiovascular health endpoints. The shape of the concentration-response curve implies that sensitivity of health effects to a unit change in PM2.5 concentration in very polluted environments is diminished compared to that in clean environments. Therefore, rather than using a continuous parametric function, we use RR lookup tables, which are provided by the GBD 2019. RRs between concentration points in the lookup tables are linearly interpolated.
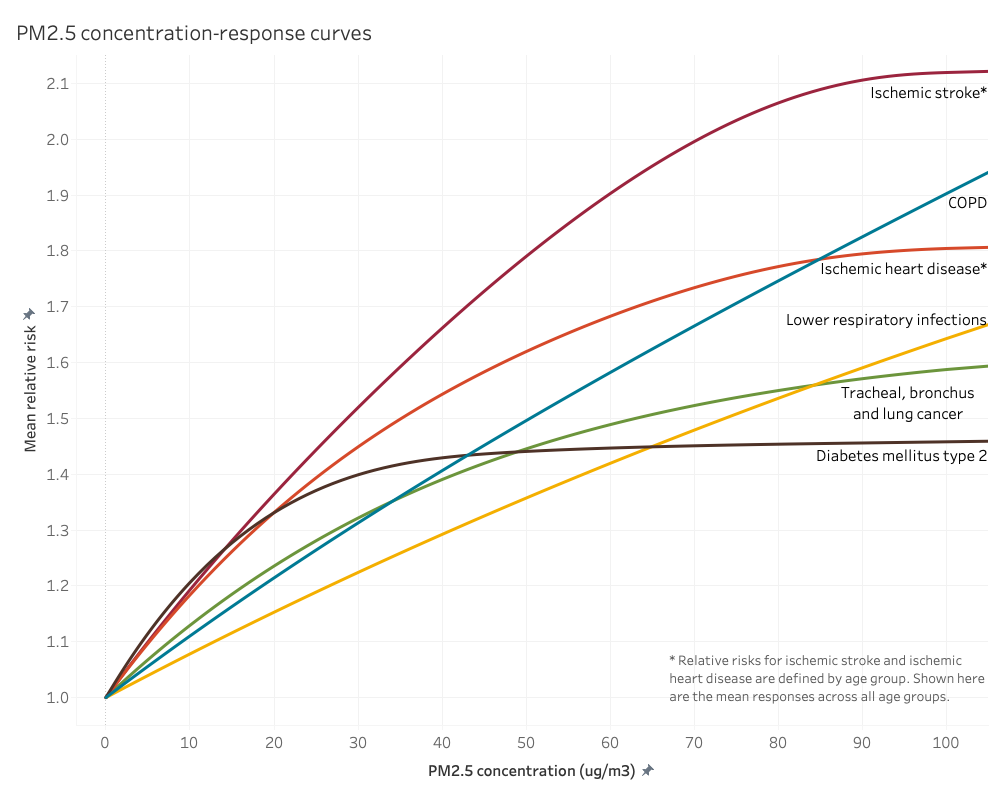
Figure 4. PM2.5 concentration-response curves for each health endpoint. Ischemic stroke and heart disease have different curves for each age group, however just the mean response is shown here.
For O3, the same RR estimate is used at all concentrations: 1.06 (95% CI 1.03, 1.10) per 10 ppb O3 increase (six-month average of the 8-hour daily maximum). This RR is based on five studies of long-term O3 exposure and COPD from Canada, the United Kingdom, and the United States. We assume the concentration-response curve for O3 is log-linear (the natural log of RR is linearly associated with O3 concentration). With this assumption, a RR of 1.06 translates to a concentration-response factor of 0.005827 (calculated by \(\ln{(\frac{\text{RR}}{10})}\)). This assumption is also used by the GBD and throughout the scientific literature.
The GBD 2019 study calculates the health burden from O3 exposure above a theoretical minimum risk exposure level (TMREL) taken from a uniform distribution between 29.1 – 35.7 ppb. We cut off any calculation of risk below the midpoint of this range, 32.4 ppb. We have decided not to use a TMREL for PM2.5 as use of the model typically focuses on smaller perturbations in concentrations well above the TMREL. In addition, epidemiological studies are finding PM2.5 mortality effects at lower and lower concentrations, down to approximately 2 µg/m3, so calculating health impacts at very low concentrations is justified by the current evidence. The TMREL is more important for O3, however, because it’s a larger fraction of the total concentration.
Future baseline disease rates
GBD 2019 gives annual baseline disease rates up to 2019, however a key feature of FATE is estimating the impacts of exposure changes into the future. In order to determine a baseline for projected disease rates we refer to the GBD Foresight project. We use their values through 2040, extending the 2040 rates forward for any years beyond. The dataset of future disease rates for each of the causes affected by air pollution was created by Rita Van Dingenen from Joint Research Centre of the European Commission. As the GBD Foresight projections were based on the GBD 2015 study, Van Dingenen scaled the original GBD Foresight future rates by the ratio of GBD 2017 to GBD 2015 values for the year 2015. Rates for diabetes mellitus type 2 are held constant at present-day levels since the Foresight project only provided future rates for type 1 and type 2 diabetes together.
Scaling was performed for each cause, land, age group:
\[\text{GBDForesight}_{\text{Scaled}(\text{Year})} = \text{GBDForesight}_{\text{Download}(\text{Year})} \times \ \frac{ {\text{GBD}2017}_{2015}}{\text{GBDForesight}_{\text{Download}(2015)}}\]We then performed further rescaling to be consistent with the GBD 2019 to avoid a substantial disconnect between historical and projected baseline rates. To rescale to the 2019 values, we first calculated the annualized percent change in Van Dingenen’s estimates from 2015-2020, 2020-2025, and so on until 2040. Then we matched these to the corresponding country-cause-age combination in the GBD 2019 data for 2019. We applied the 2015-2020 annualized rate for one year to calculate 2020 projected values from the 2019 data, then we applied the other rates to calculate annual projections to 2040.
Burden Rescaling Methods
Global Health Study burden results from GEOS-Chem use a significantly higher resolution (0.01˚x0.01˚), which means they more accurately simulate impacts on high-exposure urban areas. FATE’s burden results are rescaled to approximate the effect of the higher resolution separately by country, age group, health outcome (deaths or YLL), disease, and secondary pollutant. Burden rescaling factors are calculated by taking the ratio between baseline burden values in 2020 from FATE and GEOS-Chem when inputting GEOS-Chem’s population-weighted exposure values as an independent exposure input to FATE. These factors are constant for all model runs and, if used, are applied to the absolute burden results for all scenarios and years. With burden rescaling, FATE reproduces a country’s total avoided 2040 burden results from the Global Health Study scenarios within 13% on average.
Vsl calculation
The value of statistical life (VSL) is an economic concept that quantifies the economic value nations place on reducing the risk of premature death. It represents the monetary value that society is willing to pay to prevent a statistical average loss of life. VSL is an important tool used in cost-benefit analysis, particularly in evaluating public health and environmental regulations. The value assigned to a statistical life can vary across countries, regions, and contexts due to differences in societal values, income levels, and other cultural and economic factors.
In FATE, the calculation of VSL is an optional feature that can be performed alongside the estimation of health burden. The model takes into account the influence of a nation’s wealth on its ability to allocate resources for reducing the risk of premature death and incorporates monetary inflation over time. It is important to note that the VSL calculation in FATE focuses solely on the avoidance of premature death and does not include the added value of preventing disability.
FATE utilizes two distinct methods for the calculation of VSL to quantify the number of premature deaths by country, age, and causes. These methods are from Viscusi and Masterman (2017), referred to as the “Viscusi” method in the model, and from Narain and Sall (2016), referred to as the “World Bank” method because the World Bank published this report. Both methods involve multiplying the baseline VSL for a nation in a given year by the number of premature deaths generated by FATE’s health impacts module. However, the two methods yield different estimates due to variations in how the baseline VSL is calculated in each method.
Viscusi Method
To address the challenges of estimating VSL in different countries, Viscusi and Masterman (2017) propose a benefit transfer method that adjusts a base VSL for the United States (\(\text{VS}L_{\text{USA}}\)) of 9.6 million in 2015 USD by the relative incomes of the United States and the countries of interest.
FATE first modifies this value for baseline USA VSL into 2020 USD using the Bureau of Labor Statistics inflation rate calculator, which gives a value for an inflation factor, \(i_{2020}\), to convert from 2015 to 2020 USD. The inflation-adjusted value is further scaled to determine VSL for different countries in certain years. This scaling process involves multiplying the adjusted VSL value by the ratio of Gross National Income Per Capital, Atlas Method (GNI) of a specific country in 2015 to that of the United States. This ratio is raised to an income elasticity value, \(e\). The Viscusi method assumes that the income elasticity value is one. This assumption is based on an analysis by the authors on income data from various countries that revealed similarity in the income-to-VSL relationship compared to that of the United States, thus negating the need to raise the ratio of GNI Atlas to an exponent other than one. Further scaling by the growth rate in GNI Atlas of the country between 2015 and 2020 (\(g_{1}\)) yields the VSL in 2020 for a given country.
\[\text{VSL}_{ISO,\ 2020} = VSL_{\text{USA}} \times i_{2020} \times \left( \frac{\text{GNI}_{ISO,2015}}{\text{GNI}_{USA,2015}} \right)^{e} \times \left( 1 + g_{1,\ ISO} \right)\]The growth rate in the GNI Atlas for a specific country from 2015 to 2020, \(g_{1,\ ISO}\), is calculated as:
\[g_{1,ISO} = \frac{\text{GN}I_{2020,ISO} - GNI_{2015,ISO}{\times i}_{2020}}{\text{GN}I_{2015,ISO} \times i_{2020}}\]GNI Atlas data for most countries is collected from World Bank, with the exception of Taiwan, where national statistical data is used.
To adjust the ISO-specific VSL values from 2020 to another year, denoted \(t\), an additional growth factor, \(g_{t}\), is applied:
\[\text{VS}L_{ISO,\ t} = \text{VSL}_{ISO,\ 2020} \times (1 + g_{t,ISO})\]This adjustment considers the GNI Atlas data for a specific country in 2020, the GNI Atlas for the same country in year \(t\) and an inflation factor, \(i_{t}\), for converting from USD in 2020 to USD in year \(t\):
\[g_{t,ISO} = \frac{\text{GN}I_{t,ISO} - GNI_{2020,ISO} \times i_{t}}{\text{GN}I_{2020,ISO} \times i_{t}}\]In the Viscusi method, differences in baseline VSL for nations consider only the impact of direct currency conversion without the impact of national differences in purchasing power.
This estimate for a nation’s baseline VSL each year is multiplied by the number of premature deaths for each age category and cause, yielding total VSL from premature death by country, age, and cause.
World Bank Method
The World Bank method, based on Narain and Sall (2016), follows a similar mathematical approach as the Viscusi method but incorporates modified assumptions.
First, the base VSL value is set at 3.83 million, calculated as a World Bank average for 2011 in 2011 USD. Like the Viscusi method, the base VSL value is adjusted to 2020 USD using an inflation factor, \(i_{2020}\), from the Bureau of Labor Statistics inflation rate calculator that converts from 2011 USD to 2020 USD.
Instead of using a ratio of Gross National Income, the World Bank method utilizes a ratio of Gross Domestic Product per Capita, Purchasing Power Parity (GDP PPP) to scale the base VSL. The scaling factor is the ratio of a country’s GDP PPP in 2011 to a base GDP PPP of 37,350 for 2011 in 2011 USD, obtained from the World Bank. This scaling factor is raised to the income elasticity value, \(e\), which varies based on the income status of a country. If a country’s Gross National Income Purchasing Power Parity (GNI PPP) in 2011 exceeds 12,476 2011 USD, it is considered a high-income country, and the income elasticity is set to 0.8. For countries that do not meet the high-income threshold, the income elasticity is set to 1.2. GDP PPP and GNI PPP data are collected from the World Bank with the exception of data for Taiwan, which comes from national statistical data from the same source as in the Viscusi method.
To calculate the VSL value for a specific country in 2020, the inflation adjusted VSL value is multiplied by the income elasticity-adjusted ratio of the country’s GDP PPP in 2011 to the base GDP PPP set by the World Bank, and then multiplied by the growth rate of the country’s GDP PPP between 2011 and 2020, \(g_{1,\ ISO}\) plus one:
\[\text{VSL}_{ISO,\ 2020} = VSL_{\text{WB}} \times i_{2020} \times \left( \frac{\text{GDP PPP}_{ISO,2011}}{\text{GDP PPP}_{WB,2011}} \right)^{e} \times \left( 1 + g_{1,\ ISO} \right)\]The growth rate in the GDP PPP from 2011 to 2020 is calculated as:
\[g_{1,ISO} = \frac{\text{GDP PPP}_{2020,ISO} - \text{GDP PPP}_{2011,ISO} \times i_{2020}}{\text{GDP PPP}_{2011,ISO} \times i_{2020}}\]Subsequently, ISO-specific VSL values in other years, \(t\), for the World Bank method are determined by multiplying the VSL value in 2020 by a growth rate \(g_{t,ISO}\) of the country’s GDP PPP between 2020 and the year \(t\) as follows:
\[\text{VS}L_{ISO,\ t} = \text{VSL}_{ISO,\ 2020} \times (1 + g_{t,ISO})\]The growth rate takes into account the GDP PPP data for the specific country in 2020, the projected GDP PPP for the same country in year \(t\), and the inflation factor, \(i_{t}\), from 2020 to year \(t\):
\[g_{t,ISO} = \frac{\text{GDP PPP}_{t,ISO} - \text{GDP PPP}_{2020,ISO} \times i_{t}}{\text{GDP PPP}_{2020,ISO} \times i_{t}}\]Long-term income projections for a subset of countries come from a 2018 Organization for Economic Co-operation and Development (OECD) study for the years 2010, 2030, 2040, and 2050. Projections for the remaining countries are calculated based on Shared Socioeconomic Pathways 2 (SSP2) projections. If necessary, values are interpolated for intermediate years with growth rates adjustments.
These VSL estimates for each country in each year are then multiplied by the premature deaths generated by FATE’s health impacts module to determine associated welfare loss from premature death for each country, age category, and cause.