Polaris v1.2 Documentation
Table of contents
- Introduction
- Scope
- Overview
- Fleet turnover
- EEDI
- EEXI
- CII
- Engine and fuel switching
- Energy consumption
- Emissions
- Scenarios
Introduction
The ICCT’s Polaris model is a Python-based, global maritime emissions projection model covering all ocean transport activity. Tank-to-wake (TTW) and well-to-wake (WTW) emissions are reported as carbon dioxide equivalents (CO2e) based on the 100-year or 20-year global warming potentials of carbon dioxide, methane, nitrous oxide, and black carbon.
Polaris starts with the 2019 inventory of ~80,000 ships from ICCT’s Systematic Assessment of Vessel Emissions (SAVE) and projects its evolution out until 2070. After considering the retirement of older vessels, Polaris models the introduction of new ships to the global fleet to meet configurable demand targets. Furthermore, it allows for the investigation of the emission impacts of three key policies:
-
EEDI: A technical efficiency standard for new ships
-
EEXI: A technical efficiency standard for existing ships
-
CII: An operational efficiency standard for all ships
Customizable fuel penetration and engine retrofit shares are considered when evaluating each of the three policies. These fuel penetration and engine retrofit assumptions can be used to model the emissions consequences of fuel standards or engine replacement/retrofit policies. Polaris is highly configurable and is intended to be run with multiple policy scenarios simultaneously.
Acknowledgments
Polaris was first developed in 2022-23 by Gabe Hillman Alvarez, Xinyi Sola Zheng, Francielle Carvalho, Jakob Schmidt, Erik Pronk, Bryan Comer, and Josh Miller. Version 1.2 was developed in 2024 by Gabe Hillman Alvarez.
Scope
The fundamental unit of analysis in Polaris is the individual vessel. Nonetheless, many inputs are defined more coarsely, and it is generally useful to aggregate the outputs to inspect trends. The following conventions are used for grouping ships into classes and capacity bins.
Ship classes
The Polaris inventory is broken into two broad segments based on how ships measure their capacity: “Cargo”, which uses deadweight tonnage (DWT, a unit of mass), and “Non-cargo”, which uses gross tonnage (GT, a unit of volume). Polaris utilizes ship classes that are slightly less granular than those defined in the SAVE model. The mappings are shown below, alongside the classes defined by IMO for the purpose of EEDI regulation.
Table 1: Ship class mapping for cargo segment.
| Polaris ‘ShipClass’ | SAVE ‘ship_class’ | IMO Regulated ‘ShipTypeEEDI’ |
|---|---|---|
| Bulk carrier | bulk carrier | Bulk carrier |
| Chemical tanker | chemical tanker | Tanker |
| Container | container | Containership |
| Oil tanker | oil tanker | Tanker |
| Gas tanker | liquified gas tanker | LNG carrier |
| Other cargo | refrigerated bulk | Refrigerated cargo carrier |
| general cargo | General cargo ship | |
| other liquid tankers | N/A |
Table 2: Ship class mapping for non-cargo segment.
| Polaris 'ShipClass' | SAVE 'ship_class' | IMO Regulated 'ShipTypeEEDI' |
|---|---|---|
| Cruise | cruise | Cruise passenger ship having non-conventional propulsion |
| Ferry-pax only | ferry-pax only | Ro-ro passenger ship |
| Ferry-ro-pax | ferry-ropax | Ro-ro passenger ship |
| Ro-ro | ro-ro | Ro-ro cargo ship |
| Vehicle | vehicle | Ro-ro cargo ship (vehicle carrier) |
| Fishing | miscellaneous-fishing | N/A |
| Other non-cargo | miscellaneous-other | N/A |
| naval ship | N/A | |
| offshore | N/A | |
| service-other | N/A | |
| yacht | N/A | |
| service-tug | N/A |
Capacity bins
Ship classes are further disaggregated by capacity bins. Note that capacity bins are all defined at the SAVE ‘ship_class’ level.
Table 3: Capacity bin definitions.
| SAVE ‘ship_class’ | Capacity bin | Bin definition | Bin unit |
|---|---|---|---|
| bulk carrier | 1 | 0-9999 | DWT |
| bulk carrier | 2 | 10000-34999 | DWT |
| bulk carrier | 3 | 35000-59999 | DWT |
| bulk carrier | 4 | 60000-99999 | DWT |
| bulk carrier | 5 | 100000-199999 | DWT |
| bulk carrier | 6 | 200000-+ | DWT |
| chemical tanker | 1 | 0-4999 | DWT |
| chemical tanker | 2 | 5000-9999 | DWT |
| chemical tanker | 3 | 10000-19999 | DWT |
| chemical tanker | 4 | 20000-39999 | DWT |
| chemical tanker | 5 | 40000-+ | DWT |
| container | 1 | 0-999 | TEU |
| container | 2 | 1000-1999 | TEU |
| container | 3 | 2000-2999 | TEU |
| container | 4 | 3000-4999 | TEU |
| container | 5 | 5000-7999 | TEU |
| container | 6 | 8000-11999 | TEU |
| container | 7 | 12000-14499 | TEU |
| container | 8 | 14500-19999 | TEU |
| container | 9 | 20000-+ | TEU |
| general cargo | 1 | 0-4999 | DWT |
| general cargo | 2 | 5000-9999 | DWT |
| general cargo | 3 | 10000-19999 | DWT |
| general cargo | 4 | 20000-+ | DWT |
| liquefied gas tanker | 1 | 0-49999 | m3 |
| liquefied gas tanker | 2 | 50000-99999 | m3 |
| liquefied gas tanker | 3 | 100000-199999 | m3 |
| liquefied gas tanker | 4 | 200000-+ | m3 |
| oil tanker | 1 | 0-4999 | DWT |
| oil tanker | 2 | 5000-9999 | DWT |
| oil tanker | 3 | 10000-19999 | DWT |
| oil tanker | 4 | 20000-59999 | DWT |
| oil tanker | 5 | 60000-79999 | DWT |
| oil tanker | 6 | 80000-119999 | DWT |
| oil tanker | 7 | 120000-199999 | DWT |
| oil tanker | 8 | 200000-+ | DWT |
| other liquids tanker | 1 | 0-999 | DWT |
| other liquids tanker | 2 | 1000-+ | DWT |
| ferry-pax only | 1 | 0-299 | GT |
| ferry-pax only | 2 | 300-999 | GT |
| ferry-pax only | 3 | 1000-1999 | GT |
| ferry-pax only | 4 | 2000-+ | GT |
| cruise | 1 | 0-1999 | GT |
| cruise | 2 | 2000-9999 | GT |
| cruise | 3 | 10000-59999 | GT |
| cruise | 4 | 60000-99999 | GT |
| cruise | 5 | 100000-149999 | GT |
| cruise | 6 | 150000-+ | GT |
| ferry-ropax | 1 | 0-1999 | GT |
| ferry-ropax | 2 | 2000-4999 | GT |
| ferry-ropax | 3 | 5000-9999 | GT |
| ferry-ropax | 4 | 10000-19999 | GT |
| ferry-ropax | 5 | 20000-+ | GT |
| refrigerated bulk | 1 | 0-1999 | DWT |
| refrigerated bulk | 2 | 2000-5999 | DWT |
| refrigerated bulk | 3 | 6000-9999 | DWT |
| refrigerated bulk | 4 | 10000-+ | DWT |
| ro-ro | 1 | 0-4999 | DWT |
| ro-ro | 2 | 5000-9999 | DWT |
| ro-ro | 3 | 10000-14999 | DWT |
| ro-ro | 4 | 15000-+ | DWT |
| vehicle | 1 | 0-29999 | DWT |
| vehicle | 2 | 30000-49999 | DWT |
| vehicle | 3 | 50000-+ | DWT |
| yacht | 1 | 0-+ | GT |
| service-tug | 1 | 0-+ | GT |
| miscellaneous-fishing | 1 | 0-+ | GT |
| offshore | 1 | 0-+ | GT |
| service-other | 1 | 0-+ | GT |
| miscellaneous-other | 1 | 0-+ | GT |
Overview
The Polaris model is structured as a series of calculations that advance the fleet snapshot from year X to X + 1. Each step is described in more detail in its relevant section, but an overview is provided here as an introduction. Each year, the model executes the following instructions:
-
Apply survival curves to existing fleet and remove retired ships (this step is skipped for the base year).
-
Evaluate EEXI compliance, apply engine power limitations, enforce limits on cruise hours, and recalculate operational speed of existing ships.
-
Apply operational engine/fuel switches to existing ships.
-
Calculate regulatory and real-world emissions of existing ships and note their attained CII.
-
Apply design engine/fuel switches to possible new-build ships and generate EEDI-compliant power and speed parameters.
-
Calculate regulatory and real-world emissions for these possible new builds and note their attained CII.
-
Calculate number of actual new builds needed to fulfill demand and add them to the fleet.
Surviving and new-build ships from the previous year become the existing fleet in the next year. See Figure 1 for a graphical visualization of this numbered list.
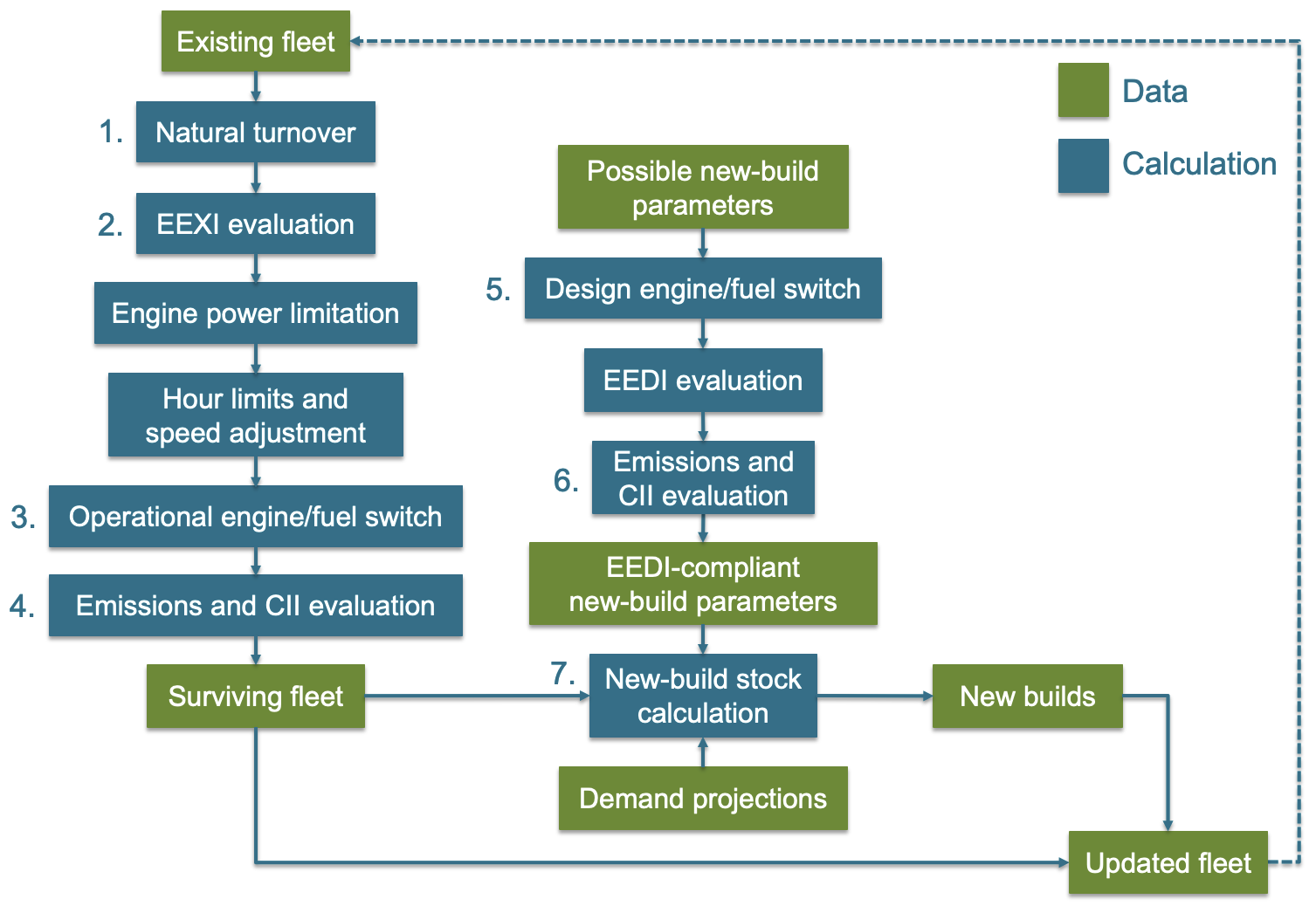
Figure 1: Model flowchart for each analysis year.
Fleet turnover
Retirements
Polaris utilizes year-over-year survival curves and pseudorandom assignment to determine which ships retire each year. The year-over-year rates of survival are calculated from 2018 and 2019 IHS Markit data and are broken down by Polaris ‘ShipClass’ and age. The survival curves define the fraction of vessels surviving from one year to the next—or similarly, the likelihood that a given vessel will survive from one year to the next. To model the behavior of individual ships, the model exploits the latter interpretation, which approaches equality with the former when there are many vessels of each class and age present in the fleet.
So, each year, a pseudorandomly-generated number between 0 and 1 is assigned to each ship and compared against the year-over-year survival rate. The ship survives if the assigned number is less than or equal to the survival rate, else the ship retires and is removed from the fleet. E.g., If the survival rate for oil tankers at age 20 is 0.95, any given 20-year-old oil tanker will retire only if its assigned number is between 0.95 and 1 (occurring about 5% of the time). Note that despite appearing random, this process is exactly reproducible by running the pseudorandom number generator with the same seed.
New-build ship parameters
The parameters of individual ships from the historical fleet are generally maintained, except when modified to comply with policies for existing ships. However, no such parameters are available for vessels that enter the fleet during modeled years, called “synthetic” ships, since they don’t yet exist in the real world or have a legitimate ship ID number. The year they enter the fleet, the synthetic ships are called “new builds”.
Most parameters for these new-build ships are calculated at a more aggregate level (SAVE ‘ship_class’ and capacity bin) as the mean values of historical ships delivered after a configurable cutoff, set to 2013 by default.
The maximum engine power and corresponding maximum cruise speed are the only new-build parameters that are not just average values from recently built ships in the corresponding bins of the historical fleet. Instead, two logarithmic regressions are performed on all ships in the base year fleet:
\[\log{\text{PowerMax}} = A*\log{\text{Capacity} + B}\] \[SpeedMax = C*\log{PowerMax + D}\]and the parameters of the resulting best-fit lines are used to calculate a more accurate estimate of the maximum power and speed of vessels as a function of ship capacity (DWT for ships in the “Cargo” segment, GT for ships in the “Non-cargo” segment). If the regressions yield an insufficiently strong correlation, a constant value is used instead. The initial estimates of new-build power and speed parameters are modified as necessary to comply with EEDI regulations.
Activity
The ship activity is an estimate of how much transport work a vessel performs in a year, taking into account the fractional payload utilization (PU, defined as the share of total capacity utilized on average). The units of activity depend on how vessels define their capacity. For ships in the “Cargo” segment, activity is measured in cargo ton nautical miles (CTnm):
\[\text{Activity}_{\text{Cargo}} = \text{DWT}*\text{PU}*\text{DistanceTraveled}\]For ships in the “Non-cargo” segment, the payload utilization is set to 1 by convention, and the activity is measured in gross ton nautical miles (GTnm):
\[\text{Activity}_{\text{Non} - \text{cargo}} = \text{GT}*1*\text{DistanceTraveled}\]New-build stock calculation
Once the supplied activity from existing ships and the parameters of possible-new build ships are defined, it is possible to determine the number of new-builds necessary to meet demand targets.
First, the additional activity needed is calculated as the difference between demand and existing supply. This demand is provided for each Polaris ‘ShipClass’ and therefore must be disaggregated by SAVE ‘ship_class’ and capacity bin to match the new-build group definition. To accomplish this, the model assumes that each of the subgroupings will retain its historical share of the total activity of its umbrella group (e.g., ‘general cargo’ bin 4 will always be assigned 75% of the additional activity needed from ‘Other cargo’).
Finally, the assigned activity is converted into stock by dividing by the average activity of each vessel in that ‘ship_class’ and bin. This mean value and the activity shares both come from a historical sample subject to the same configurable cutoff as described above (default 2013).
\[\text{NewBuildStock}_{\text{ship}\text{_}class,Bin} = \frac{\text{ActivityNeeded}_{\text{ShipClass}}*\text{ShareOfActivity}_{ShipClass \rightarrow ship\text{_}class,Bin}}{\text{MeanActivityOfVessel}_{\text{ship}\text{_}class,Bin}}\]New-build stock at the bin-level is further disaggregated by shares of main engine and primary (and potentially secondary) fuel types, rounded to the nearest integer, and then separated into individual vessels (initially identical, but may evolve differently).
EEDI
Required EEDI
Polaris applies the IMO’s Energy Efficiency Design Index (EEDI), as defined in MEPC.328(76), to all possible new-build ships before estimating their activity and determining necessary stock.
New-build ships are assigned an EEDI reference line (see Table 2 under Regulation 24 in resolution 328(76), linked above), EEDI phase, and reduction factor (Regulation 24 Table 1), from which required EEDI is calculated:
\[Required\ EEDI = \left( 1 - \frac{X}{100} \right)*\ EEDI\ reference\ line\ value\]where X is the reduction factor from the reference line.
Attained EEDI
The IMO defines the full equation for attained EEDI in MEPC.308(73), but Polaris uses a simplified version, based on Equation 1 from a previous ICCT analysis (Rutherford et al., 2020):
\[\text{Attained}\ \text{EEDI} = \frac{C_{f}*(P_{\text{ME}}*\text{SFC}_{\text{ME}} + P_{\text{AE}}*\text{SFC}_{\text{AE}}\text{)}}{Capacity\ *V_{\text{ref}}}\]where the constituent variables are defined as follows:
-
\(C_{f}\ \): fuel carbon factor (gCO2/g fuel)
-
\(P_{\text{ME}}\ \): 75% of maximum main engine power (kW)
-
\(\text{SFC}_{\text{ME}}\) : specific fuel consumption of main engine (g fuel/kWh)
-
\(P_{\text{AE}}\ \): auxiliary engine demand in cruise phase (kW)
-
\(\text{SFC}_{\text{AE}}\) : specific fuel consumption of auxiliary engine (g fuel/kWh)
-
\(\text{Capacity}\) : DWT, except for containerships (70% of DWT) and cruise ships (GT)
-
\(V_{\text{ref}}\) : reference speed associated with \(P_{\text{ME}}\) (knots)
In the case that attained EEDI exceeds required EEDI, we assume that shipbuilders achieve compliance by installing a smaller main engine, thereby decreasing the maximum main engine power (a.k.a. maximum continuous rating, \(M\text{CR}\)) and maximum speed. This in turn decreases \(P_{\text{ME}}\), and, to a lesser extent, \(V_{\text{ref}}\). For consistency with the EEXI calculations, we call this an “EEDI engine power limitation (EPL)”. The critical adjustment is:
\[\text{MC}R^{'} = MCR*\left( 1 - \text{EPL}_{\text{EEDI}} \right)\]where the apostrophe denotes an updated parameter.
For the purposes of attained EEDI, the reference parameters are evaluated at 75% of maximum engine power. So, the EEDI reference speed is defined as:
\[V_{\text{ref}} = {(0.75)}^{1/3}*\text{MaxSpeed}\]with the implicit assumption that main engine power scales with the cube of speed. This reference speed is recalculated if the maximum speed is altered by an EEDI EPL:
\[MaxSpeed' = MaxSpeed*\left( 1 - E\text{EPL}_{\text{EEDI}} \right)^{1/3}\] \[V_{\text{ref}}' = \left( 0.75 \right)^{1/3}*\text{MaxSpeed}'\]Note that, in contrast to speed, the reference engine power scales linearly with EEDI EPL:
\[P_{\text{ME}}' = {0.75*\text{MCR}' = P}_{\text{ME}}*(1 - \text{EPL}_{\text{EEDI}})\]The EEDI EPL may be arbitrarily close to zero but is not allowed to exceed a configurable limit, set to 60% by default. New-build ships which cannot be made to comply with EEDI via this scheme are flagged for the user and built to be as close to compliance as possible.
EEXI
Required EEXI
The Energy Efficiency Existing Ship Index (EEXI) is defined alongside EEDI in MEPC.328(76) and uses the same EEDI reference lines, but incorporates a different set of reduction factors (Table 3 under Regulation 25). Polaris applies EEXI to all existing ships, both historical (i.e., present in the base-year fleet) and synthetic (i.e., introduced during modeled years). Required EEXI is given as:
\[\text{Required}\ E\text{EXI} = \left( 1 - \frac{Y}{100} \right)*\ EEDI\ reference\ line\ value\]where Y is the reduction factor specified for the required EEXI compared to the EEDI reference line. To date, EEXI is less stringent than the EEDI, so new ships will comply with the EEXI by virtue of complying with the EEDI.
Attained EEXI
The full equation for attained EEXI is given in MEPC.333(76), but we utilize the same simplification as for attained EEDI:
\[Attained\ EEXI = \frac{C_{f}*(P_{\text{ME}}*\text{SFC}_{\text{ME}} + P_{\text{AE}}*\text{SFC}_{\text{AE}}\text{)}}{Capacity\ *V_{\text{ref}}}\]where all the variables are also defined as for EEDI, except for \(P_{\text{ME}}\) and \(V_{\text{ref}}\) (details below). In the case that attained EEXI is greater than the required EEXI, the model assumes that ship operators achieve compliance by placing an overridable limit on main engine power, called an “EEXI engine power limitation (EPL)”, which limits the engine’s maximum continuous rating (\(\text{MCR}\)) by a percentage (\(\text{EPL}_{\text{EEXI}}\)) as follows:
\[\text{MCR}_{\text{EPL}} = \text{MCR}*(1 - \text{EPL}_{\text{EEXI}})\]Note that the ship’s maximum installed power (\(\text{MCR}\)) and speed (\(\text{MaxSpeed}\)) are not themselves affected by an EEXI EPL, so the \(\ _{\text{EPL}}\) subscript is used instead of an apostrophe to denote an updated reference parameter only.
For the purposes of attained EEXI, the reference parameters are evaluated at 83% (not 75%) of the limited maximum main engine power (\(\text{MCR}_{\text{EPL}}\)). This change in evaluation point reflects the assumption that ships will operate closer to the compliance-limited maximum power than they did to the previously unrestricted maximum power.
To ensure that an EEXI EPL does not cause ships’ technical efficiency to worsen, consistent with IMO guidelines, cases where 83% \(\text{MCR}_{\text{EPL}}\) would be greater than 75% \(\text{MCR}\) are not allowed. This constraint establishes a minimum EEXI EPL of about 10%. Ships that could comply with an EEXI EPL smaller than the minimum are considered compliant without needing to alter their operations. For ships requiring an EPL larger than the minimum, the updated reference parameters are given by:
\[P_{\text{ME},\ \text{EPL}} = 0.83\ \text{MCR}_{\text{EPL}}\] \[V_{\text{ref},\ \text{EPL}} = {(0.83)}^{1/3}*\text{MaxSpeed}*\left( 1 - \text{EPL}_{\text{EEXI}} \right)^{1/3}\]The EEXI EPL is also not allowed to exceed a configurable limit, set to 60% by default. Existing ships which cannot be made to comply with EEXI via this scheme are flagged for the user and retired.
Engine power limitation
Each ship class and capacity bin has a default distribution of main engine power load factors that defines the fraction of total cruise hours that ships in that class and bin spend at different engine powers. Default distributions for three major ship classes (aggregated over all capacity bins) are shown in Figure 2 as an example. An individual vessel’s distribution may be affected by an EEXI EPL as follows:
-
For each load factor bin with corresponding engine power exceeding the new limited maximum (\(\text{MCR}_{\text{EPL}}\)), the share of hours is set to zero, since the ship is no longer allowed to operate at that power.
-
The sum of shares from all disallowed load factor bins is added to the bin corresponding to the greatest load factor which does not exceed the new limited maximum.
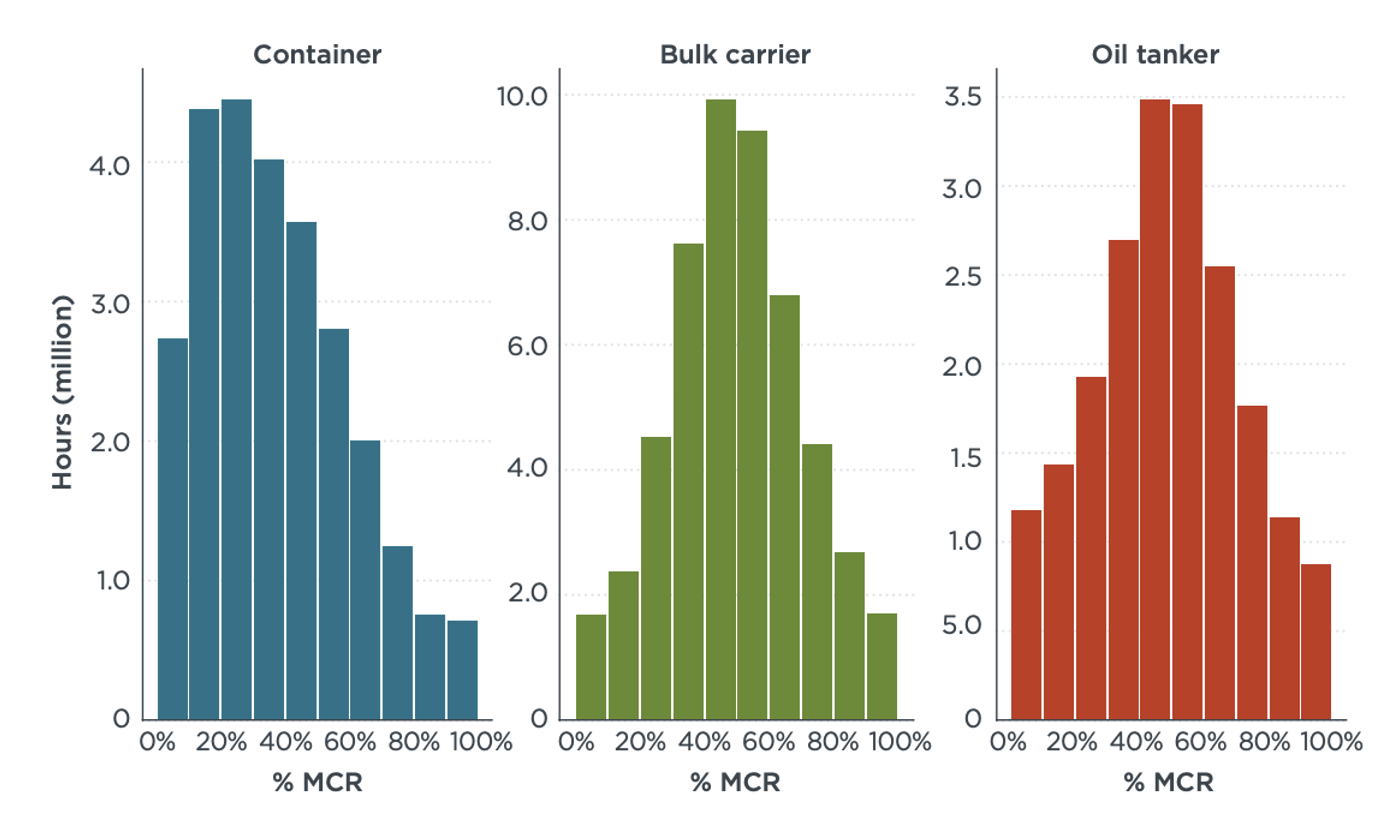
Figure 2. Some default main engine load factor distributions (Rutherford et al., 2020).
By default, 10 bins are used, and each is defined by its midpoint (e.g., 0.75 corresponds to the range \(0.70, 0.80\)), although users may provide custom bins. For example, if a ship has an EEXI EPL of 21%, then \(\text{MCR}_{\text{EPL}}\) = 79% MCR, and any hours which would normally be operated at 95% and 85% MCR are instead operated at 75% MCR.
Operational speed reduction
Once the main engine power load factor distribution is updated with an EEXI EPL, the average cruise speed is calculated as:
\[MeanCruiseSpeed = MaxSpeed*\sum_{\text{LoadFactors}}^{}\left( \text{LoadFactor}^{\frac{1}{3}}*ShareOfHours_{\text{LoadFactor}} \right)\]where the sum is over all load factors and the share refers to the share of hours operated at that load factor.
Excess hours
The total hours operated in cruise phase is calculated from the mean cruise speed as:
\[Total\ cruise\ hours = \frac{\text{Distance}\ \text{traveled}}{\text{Mean}\ \text{cruise}\ \text{speed}}\]Since the distance traveled by a ship is not adjusted by EEXI, an EPL will therefore decrease the mean cruise speed and increase the total cruise hours. Since there are only so many extra hours a vessel can operate in a year, this cruise hours estimate is capped at the 99th percentile values by ship class from the SAVE 2019 fleet.
This limit may generate excess hours, which correspond to activity which cannot be completed by the affected ship and must instead be allocated to new ships. The calculation is done vessel-by-vessel as follows:
\[Excess\ hours = Total\ cruise\ hours - Maximum\ cruise\ hours\] \[Distance\ traveled' = Distance\ traveled - Excess\ hours*Mean\ cruise\ speed\] \[\text{Activit}y^{'} = \ Activity*\ \frac{\text{Distance}\ t\text{ravele}d'}{\text{Distance}\ \text{traveled}}\]If there is stable or increasing demand, this reduction in activity from existing ships is automatically converted into increased activity from new-build ships in the new-build stock calculation.
CII
Polaris applies IMO’s Operational Carbon Intensity Indicator (CII), which quantifies the average CO2 emissions per transport work of a ship. The CII applies to all ships 5,000 GT and above in the following ship classes: bulk carriers, gas carriers, tankers, container ships, general cargo ships, refrigerated cargo carriers, combination carriers, LNG carriers, vehicle carriers, Ro-Ro cargo vessels, Ro-Ro passenger vessels and cruise ships.
CII reference line
For each applicable ship class, the model first calculates its CII reference line, as defined in MEPC.337(76). Each reference line is given as a curve representing the median attained operational carbon intensity performance in 2019, as a function of ship capacity. The reference lines are calculated as follows:
\[\text{CII}_{\text{Ref}} = a*\text{Capacity}^{- c}\]where Capacity is the DWT or GT of a ship, and a and c are parameters estimated by IMO through median regression fits on the 2019 data.
Required CII
Polaris then calculates the required annual operational CII as defined in MEPC.338(76). The required CII is determined based on percentage of reduction from the CII reference line:
\[Required\ annual\ operational\ CII = \left( 1 - \frac{Z}{100} \right)*\text{CII}_{\text{Ref}}\]where \(\text{CII}_{\text{Ref}}\) is the reference value as described above, and Z is the reduction factor.
The stringency of CII (i.e., reduction factor) starts at 5% in 2023 and increases gradually to 11% in 2027. Although the policy does not go into effect until 2023, Z factors of 1%, 2% and 3% were set by IMO for the years of 2020, 2021, and 2022, respectively. Z factors for years beyond 2027 will be developed as the CII is reviewed and revised. For modeling purposes, Polaris holds the required CII at an 11% reduction from the reference line from 2027 onwards.
Attained CII
As defined in MEPC.366(76), the attained annual operational CII of individual ships is calculated as the ratio of the total mass of CO2 (M) emitted to the total transport work (W) undertaken in a given calendar year, as follows:
\[Attained\ CII = M/W\]The mass of CO2 emissions (M) is calculated by summing the CO2 emissions (in grams) from all the fuel oil consumed on board a ship in a given calendar year. For each ship, the model multiplies its total fuel energy consumption with a weighted average emission factor, as detailed in the Emission section below.
Transport work (W) is defined as the product of a ship’s capacity and the distance travelled in a given calendar year:
\[W = Capacity*DistanceTraveled\]where Capacity has units of DWT or GT depending on the ship class, and the distance is in nautical miles.
CII rating
Each ship is also assigned an attained CII rating. As described in MEPC.339(76), four rating boundaries (superior, lower, upper, and inferior) are defined to sort ships into the five-grade rating system (A, B, C, D, and E).
The boundaries are set based on the distribution of attained CIIs of individual ships in 2019. Mathematically, the boundaries are determined by the required CII and a set of deviation vectors (d1, d2, d3, and d4) that indicate the direction and distance they deviate from the required value, as illustrated in Figure 3:
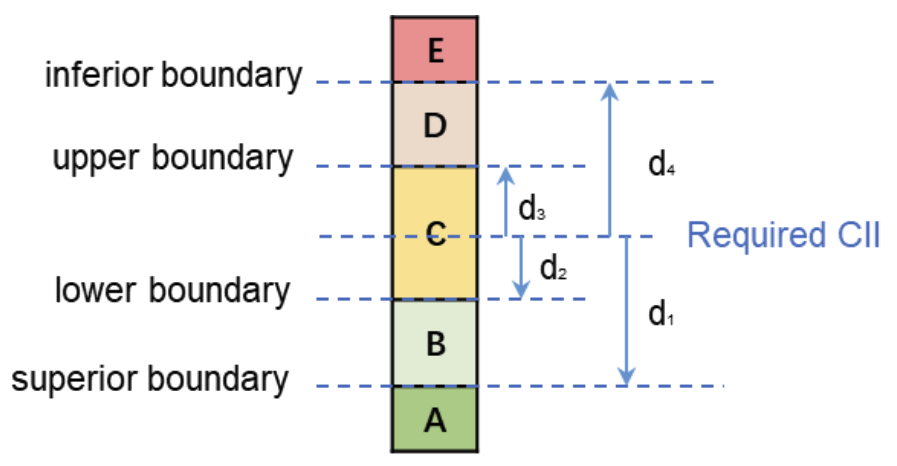
Figure 3. CII boundaries (Resolution MEPC.354(78)).
Based on an exponential transformation of the deviation vectors and the required CII, the four rating boundaries can be calculated as follows:
\[Superior\ boundary = \exp\left( d_{1} \right)*Required\ CII\] \[Lower\ boundary = \exp\left( d_{2} \right)*Required\ CII\] \[Upper\ boundary = \exp\left( d_{3} \right)*Required\ CII\] \[Inferior\ boundary = \exp\left( d_{4} \right)*Required\ CII\]Each ship is assigned a CII rating based on which boundaries they fall within. Note that unlike EEXI, this CII rating is not assumed to directly influence ship behavior in Polaris. CII ratings are calculated and reported to the user, and they may be used to inform engine/fuel switching choices for successive runs of the model. For example, if a particular bin of ships is skewing towards worse CII ratings in a given year, the user may choose to increase the share of ships from that bin which switch to lower-emission fuels in that year.
Engine and fuel switching
To comply with EEDI and EEXI or to achieve a higher rating under CII, ship operators may switch to a more efficient engine, a lower emission fuel source, or both at the same time. Polaris models such behavior based on estimated rates of engine installations/retrofits and fuel switching in each calendar year at the fleet level, rather than ship-by-ship.
Each year, the model takes in a list of possible switches for each ship class and each size bin. The “switch map” is necessary because not all engine options and fuel options are compatible with each other. For one existing engine and fuel combination, multiple replacement options may exist.
The design engine and fuel are used for EEDI and EEXI calculations, whereas the operational engine and fuel are used for CII and emissions calculations.
Design engine and fuel switching
For EEDI compliance, a ship operator may decide to purchase new-build ships with alternative engine and fuel combinations. Each year, the Turnover module calculates the number of new-build ships needed based on ship retirement and projected demand, and it initially assumes that all new builds follow the engine and fuel distributions of that ship class in the previous year.
Based on user input, the model then takes a certain share of the default new-build ships and converts them to use an alternative combination of engine and fuel. To model the use of drop-in alternative fuels, Polaris distinguishes between primary and secondary fuels, with a user-specified blend ratio between the two.
Operational engine and fuel switching
For EEXI compliance or achievement of higher CII rating, a ship operator may change the operational engine and fuels of an existing, in-service ship. For ships in the same segment (those in the same ship class and size bin and have the same design engine and fuel configuration), a pseudorandomly-generated number between 0 and 1 is assigned to each ship and compared against the share of various switch options provided by user.
For instance, the user may specify that 50% of the ships in a particular segment are not switching engines or fuels, 30% are switching to option A, and the remaining 20% are switching to option B. In this case, ships assigned values between 0 and 0.5 would not change configuration, those assigned values between 0.5 and 0.8 would switch to option A, and the rest of the ships would switch to option B. Note that despite appearing random, this process is exactly reproducible by running the pseudorandom number generator with the same seed.
Energy consumption
Main engine in cruise phase
Similar to average operational speed, the total energy consumed by the main engine in cruise phase is calculated as a sum over main engine power load factor (\(\text{Lf}\)) conditions. The product of the load factor and maximum power output of the main engine gives the power output of the main engine at that load factor, and the product of total cruise hours with the share of hours spent in that load factor bin gives the number of hours operated in that load factor bin. The product of the specific fuel consumption and the fuel energy content gives an inverse engine efficiency which converts from energy out of the engine to energy into the engine. So, the full equation is written as:
\[\text{EnergyConsumed}_{\text{Main}}\left\lbrack MJ_{\text{in}} \right\rbrack \\ = \sum_{\text{Lf}}^{}{\left( Lf*{\text{MaxPowerOutpu}t_{\text{Main}}\left\lbrack kW_{\text{out}} \right\rbrack*ShareOfHours}_{\text{Lf}}*CruiseHours\ \left\lbrack \text{hr} \right\rbrack \\ *SpecificFuelConsumption_{\text{Lf}}\left\lbrack g/kWh_{\text{out}} \right\rbrack*FuelEnergyContent\ \left\lbrack MJ_{\text{in}}/g \right\rbrack \right)\ }\]where the specific fuel consumption of the main engine varies with load factor according to the relationship established in the Third IMO GHG Study 2014:
\[\text{SpecificFuelConsumptio}n_{\text{Lf}} \\ = SpecificFuelConsumption_{\text{Baseline}}*(0.455*Lf^{2} - 0.71*Lf + \ 1.28)\]Auxiliary engines, boilers, and non-cruise phases
The hours spent in phases other than cruise (namely, anchor, berth, and maneuver) are defined by estimates from the SAVE 2019 fleet and assumed not to change. The main engine is assumed to only operate during cruise phase. The average energy demand on the auxiliary engines and boilers in each phase, including cruise, is also derived from the SAVE 2019 fleet and left unmodified. The efficiencies of auxiliary engines and boilers are also assumed to be constant. So, for auxiliary engines and boilers, the energy consumption is given by:
\[\text{EnergyConsumed}_{EnergyConsumer,Phase}\left\lbrack MJ_{\text{in}} \right\rbrack \\ = MeanPowerDemand \left\lbrack kW_{\text{out}}\right\rbrack * \text{HoursInPhase} \left\lbrack \text{hr} \right\rbrack \\ * \text{SpecificFuelConsumption} \left\lbrack g/kWh_{\text{out}} \right\rbrack * \text{FuelEnergyContent} \left\lbrack MJ_{\text{in}}/g \right\rbrack\]The total energy consumed by all energy consumers in all phases is tabulated by summing up the energy consumed by main engines, auxiliary engines, and boilers in each phase.
Emissions
Carbon dioxide equivalent (CO2e) emissions are calculated from energy consumption using emission factors:
\[Emissions = Energy\ consumed*Emission\ factor\]Weighted average emission factors
Polaris allows ships to be modeled with both a primary and secondary fuel. The emission factors are therefore an average of the values for the two fuels, weighted by the energy provided by each. E.g., if a ship derives 70% of its energy, measured in megajoules (MJ), from fuel A (emission factor = 1 g/MJ) and the other 30% from fuel B (emission factor = 0 g/MJ), the weighted average emission factor would be 0.7 g/MJ. Note that this calculation assumes that auxiliary engines and boilers use the same blend of fuels as the main engine.
Regulatory vs. estimated real-world emissions
Polaris allows a variety of scopes of emissions, generally falling into two broad categories: regulatory and real-world. Regulatory emissions are calculated using the official emission factors listed in IMO policies, which currently reflect only the tank-to-wake (TTW) scope.
Although the model uses regulatory emission factors for the EEDI, EEXI, and CII compliance calculations, it also allows the user to add well-to-tank (WTT) emission factors and to modify the default TTW emission factors to produce estimated real-world well-to-wake (WTW) emissions.
Scenarios
Polaris comes pre-packaged with a robust set of default data to allow for quick modeling of baseline trends. Users can provide inputs defining alternate scenario pathways or updating baseline assumptions.
Scenario inputs
Polaris currently allows each of the inputs defined in Table 4 to vary between multiple scenarios in a single model run.
Table 4: Scenario input descriptions.
| Scenario Input | Description |
|---|---|
| payload_utilization | Payload utilization projections file. Subject to the upper limits defined for that ship class and year |
| demand | Projection of demand for transport work (t-nm). For cargo ships, demand is based on cargo tonnes; for non-cargo ships, it is based on gross tonnes |
| design_fuel_switch | Specifies the design engine and fuels of new-build ships |
| design_fuel_blend | Specifies the blend between the alternative main and secondary fuels of new-build ships defined in the design fuel switch input |
| op_fuel_switch | Alters the operational engine and fuels of all existing ships |
| op_fuel_blend | Defines the blend between the alternative main and secondary fuels defined in the operational fuel switch input for all ships |
| eedi_on | Toggles on/off enforcement of EEDI requirements for new-build ships (on by default) |
| eexi_on | Toggles on/off enforcement of EEXI requirements for existing ships (on by default) |
| max_epl | Configurable upper limit on maximum engine power limitation allowed to comply with EEDI/EEXI policies (default 60%) |
| eedi_required | Custom modifications to required EEDI reductions from reference lines |
| eexi_required | Custom modifications to required EEXI reductions from EEDI reference lines |
Default inputs
The default data used to define the baseline (a.k.a. business-as-usual or BAU) scenario are described in Table 5. Sources are included for transparency and replicability. See relevant sections above to learn more about how each input is used in the model.
Table 5: Default input descriptions and sources.
| Input | Description | Source |
|---|---|---|
| base_fleet | Base year fleet inventory from SAVE database | SAVE 2019 – Olmer et al. (2017) Fourth IMO GHG Study – Faber et al. (2020) |
| size_bin | SAVE capacity bin definitions with corresponding boiler and auxiliary power demand | Olmer et al. (2017) |
| survival_curves | Fleet survival curves by ship class | 2018 and 2019 data from IHS Markit ShipData database (bespoke database purchased by the ICCT) |
| engine_shares | Engine and fuel share projections for new builds | Forward filled from SAVE 2019 - Olmer et al. (2017) |
| sfc | Specific Fuel Consumption of main and auxiliary engines | SSD, MSD, HSD, LNG-Otto-medium/slow, LBSI, GT, ST (Distillate, Residual, or LNG) – Faber et al. (2020) SSD or MSD running on methanol – MAN Engine’s calculation tool Fuel cells (hydrogen, ammonia) – Marine Service Noord and Comer et al. (2022) ST (nuclear, coal) - World Nuclear and U.S. EIA |
| fuel_efs | Emission factors for different fuels | Distillate and Residual – Faber et al. (2020) and GREET (2021) LNG and Bio-LNG - Comer et al. (2022) and GREET (2022) Biofuels - GREET (2021) Methanol, Biomethanol and E-methanol - GREET (2021) Hydrogen and Ammonia - GREET (2021) Coal – GREET (2021) Nuclear - Center for Sustainable Systems (2021) |
| demand | Demand for transport work | UNCTAD (2021) |
| payload_utilization | Share of total capacity utilized on average | UNCTAD (2021) and Olmer et al. (2017) |
| payload_utiization_limit | Realistic upper limit for payload utilization | 105% of historical maximums from 2013-2019, via UNCTAD (2021) |
| new_build_param | Estimated parameters for synthetic ships such as maximum engine power | Extrapolated from historical data – IHS ShipData database and Olmer et al. (2017) |
| power_speed | Linear regression for PowerMax and SpeedMax parameters | Olmer et al. (2017) |
| hours_by_phase | Annual hours spent in each phase | Olmer et al. (2017) |
| max_cruise_hours | Historical upper limits on operating hours | Olmer et al. (2017) |
| load_factor_bins | Definitions of load factor bins used in power distribution | Olmer et al. (2017) |
| power_dist | Distribution of operational power load factors | Olmer et al. (2017) |
| eedi_reference_lines | Definitions of EEDI reference lines | Resolution MEPC.231(65) |
| eedi_required | Required EEDI reductions from reference lines | Resolution MEPC.328(76) |
| eexi_required | Required EEXI reductions from EEDI reference lines | |
| cii_capacities | Capacities for use in CII calculations | Resolution MEPC.353(78) |
| cii_reference_lines | CII reference lines | Resolution MEPC.353(78) |
| cii_required | Required CII reductions from reference lines | Resolution MEPC.338(76) |
| cii_rating | Definitions of CII ratings | Resolution MEPC.354(78) |