FATE v1.0 Documentation
06/01/2023
Table of contents
- Introduction
- Air quality methods
- Perturbing emissions
- Health impact assessment methods
- VSL calculation
Introduction
The Fast Assessment of Transportation Emissions (FATE) model evaluates air quality and health impacts associated with present or future changes in air pollutant emissions from 9 sectors, including 3 transportation sub-sectors. The tool estimates the national population-weighted ambient PM2.5 exposure (annual average in µg/m3) for 181 countries and ozone (O3) exposure (6-month average of the 1hr or 8h daily maximum O3 in ppb) for 19 individual G20 countries and 24 additional EU member countries. It also outputs the number of premature deaths and disability-adjusted life years (DALYs) associated with exposure to these two pollutants. Supplementary outputs of the tool include national baseline exposures to ambient PM2.5 and O3 and detailed health impacts by ambient pollutant, disease, and age group. Health outputs of the tool also include 5th and 95th percentile estimates that reflect uncertainty in the concentration-response relationship. FATE also optionally quantifies the number or premature deaths to a dollar amount using the Value of a Statistical Life (VSL) using two methods.
FATE is a reduced-complexity air quality model, allowing users to simulate national, regional, or global scenarios without the high computational costs usually required by chemical transport models. The extent to which exposures of PM2.5 and O3 respond to changes in emissions of primary pollutant species, denoted as sensitivities, are calculated using the adjoint of the GEOS-Chem model. The health impacts associated with exposure to these pollutants are calculated using methods consistent with the Global Burden of Disease (GBD) 2019. The tool is designed to accommodate future updates to GBD health impact assessment methods. To estimate health impacts in future years, the tool considers projected changes in population, age distributions, and baseline disease rates at the national level.
FATE evaluates the impact of emission changes by comparing health burden and exposure in a user-specified scenario to the burden and exposure of FATE’s built-in baseline. The baseline emissions projections used in FATE are derived from the ECLIPSE V5a Reference scenario. ECLIPSE classifies gridded emissions into 7 primary pollutant species and 9 source sectors, with a spatial resolution of 0.1° × 0.1°. FATE includes annual ECLIPSE baseline emissions data for the years 2015, 2020, 2030, 2040, and 2050, while values for intermediate years are interpolated.
Users can input absolute (tonnes, kt, or \(kg/m^{2}\)) or relative (fractional) changes to ECLIPSE emissions. These emissions can be specified either at the country scale, where gridding algorithms are applied using the built-in country map, or in user-specified grid cells. Users have the choice of using the GEOS-Chem global 2° × 2.5° grid or the ECLIPSE 0.1° × 0.1° grid for defining grid cells. Emissions can be perturbed for any year between 2015 and 2050. If users are confident that their emissions accurately represent total-sector emissions, they have an additional option replace the ECLIPSE baseline for specific species, sectors, countries (or grid cells), and years using the independent emissions input option. The tool provides the flexibility to run either a single scenario or a batch including multiple scenarios.
FATE provides the most detail within the transportation sector; however, there are no limitations preventing analyses of other supported sectors as well while considering model assumptions. Detailed information regarding the supported sectors and emission species can be found in the sections below.
Sectors
ECLIPSE data classifies emissions based on their sources, breaking down each primary pollutant species by sector. The sectors, including four specific to transportation, are listed in the table below. On-road transport is encompassed by diesel and gasoline sectors (TRA_MD, and TRA_GSL), while the shipping sector (SHP) represents emissions from maritime shipping. The other transportation sector (TRA_OTH) includes aviation and other forms of off-road transport, excluding maritime shipping. It’s worth noting that upstream emissions associated with one sector but produced by another sector are considered within the emissions of the sector that directly produces those emissions. For instance, the emissions from electricity generation used to power electric vehicles are accounted for in the energy sector’s emissions, not in the transportation sector’s.
| Abbreviation | Description |
|---|---|
| WST | Waste |
| AGR | Agriculture |
| ENE | Energy |
| IND | Industry |
| RES | Residential |
| SHP | Shipping |
| TRA_GSL | Road transport gasoline (+ other non-diesel fuels) |
| TRA_MD | Road transport diesel |
| TRA_OTH | Other non-road transport (but excluding all shipping) |
In FATE, perturbations are applied to specific sectors, species, ISOs, or grid cells. When applying ISO-specific perturbations, users should consider the sector being perturbed, as ISO-specific perturbations only affect emissions within the land area and borders of the given ISO. Specifically, emissions from the SHP and TRA_OTH sectors, which are not confined solely to land-based activities, extend beyond national borders. Therefore, it is recommended to utilize a gridded perturbation or apply perturbations globally when dealing with these sectors.
Species
FATE quantifies health burden by assessing a population’s exposure to PM2.5 and O3, which are secondary pollutants formed in the atmosphere from primary emissions by vehicles and other sources. While certain sectors directly emit PM2.5, it is generally understood that the contribution from primary emissions within the transportation sectors is relatively small compared to secondary production.
PM2.5 refers to fine particulate matter with a diameter of 2.5 micrometers or smaller. As PM2.5 encompasses particles of various molecular compositions, its production can originate from diverse sources. Primary black carbon (BC) and organic carbon (OC) contribute to the formation of secondary organic aerosols (SOA), which are a significant component of PM2.5. Additionally, ammonia (NH3) reacts with sulfur dioxide (SO2) and nitrogen oxides (NOx) to generate ammonium sulfate (NH4HSO4) and ammonium nitrate (NH4NO3) particles, further contributing to the concentration of PM2.5. In FATE, BC, OC, NH3, NOx, and SO2 are considered precursor species in the production of PM2.5.
Ozone (O3) is formed through photochemical reactions involving NOx and volatile organic compounds (VOCs). Carbon monoxide (CO) indirectly influences the production of these secondary pollutants through its participation in atmospheric reactions. In FATE, NOx, VOC, and CO are considered precursor species in the production of O3.
| Abbreviation | Chemical species | Emitted species |
|---|---|---|
| BC | Primary black carbon | Carbon (C) |
| OC | Primary organic carbon | Carbon (C) |
| NH3 | Ammonia | Ammonia (NH3) |
| NOx | Nitrogen oxides | Nitrogen (N) |
| SO2 | Sulfur dioxide | Sulfur dioxide (SO2) |
| CO | Carbon monoxide | Carbon monoxide (CO) |
| VOC | Non-methane volatile organic compounds | ≥C4-alkanes, formaldehyde (HCHO), ethane (C2H6), propane (C3H8), propene (C3H6), acetone, methyl ethyl ketone and acetaldehyde (all units are C) |
Air quality methods
FATE utilizes sensitivities derived from the adjoint of the GEOS-Chem model to estimate national population-weighted concentrations of PM2.5 and O3. The adjoint of the GEOS-Chem model identifies the emission sources that contribute to exposure by calculating the sensitivity of a nation’s population-weighted pollutant exposure (PM2.5 or O3) to an emissions perturbation in any of the global model’s 2° × 2.5° grid cells. These sensitivities, output as gridded coefficients from the GEOS-Chem adjoint, approximate the effects of pollutant dispersal, secondary pollutant formation, and population distribution on exposure. Utilizing these coefficients simplifies the population-weighted exposure calculation in FATE, reducing it to a simple multiplication:
\[Exposure = Adjoint\ Sensitivities \times Perturbed\ Emissions\]It is important to note that the adjoint calculation provides a local linear approximation of the sensitivity used in GEOS-Chem, resulting in some uncertainty when modeling large emission perturbations. The perturbed emissions are re-gridded to match the 2° × 2.5° resolution of the adjoint sensitives and multiplied element-wise. This calculation results in a gridded exposure at 2° × 2.5°, which is then aggregated to the national level for the calculation of health impacts.
The adjoint sensitivities are calculated for chemical species, thus they do not vary by sector. These coefficients are provided as 2D arrays for surface-layer emissions. When applying these sensitivities to calculate impacts from sectors such as aviation, it is important to consider the assumption of surface emissions. Since aviation releases emissions at higher altitudes, the pollutant response may vary compared to the same mass of emitted species from a sector emitting solely at the surface.
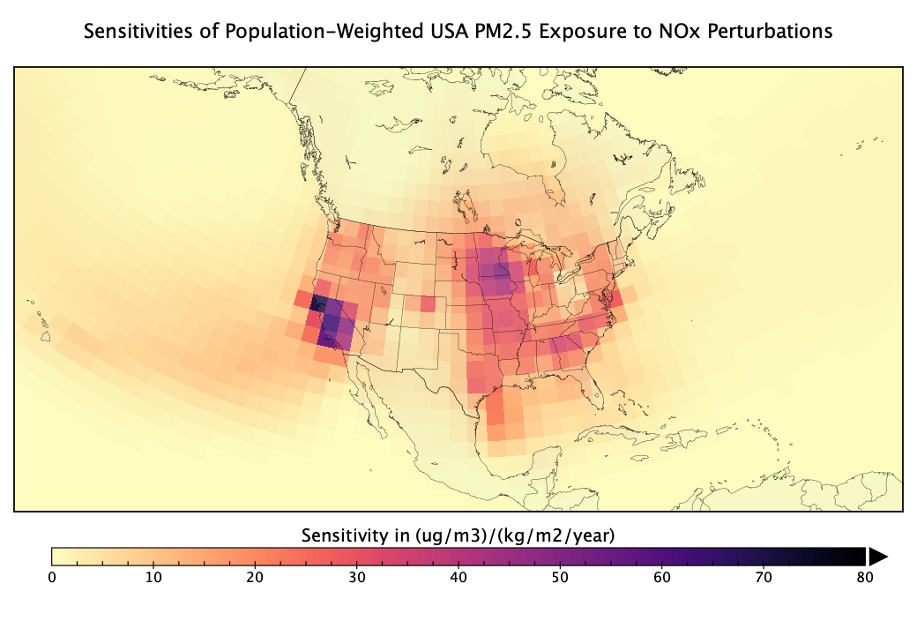
Figure 1. Subset of USA PM2.5 adjoint sensitivities for NOx emissions. Values represent the degree to which gird cells are sources of NOx that contribute to population-weighted PM2.5 exposure in the United States.
PM2.5
The adjoint response coefficients for the PM2.5 calculations give the sensitivity of population-weighted annual average PM2.5 to emissions of BC, OC, NH3, NOX, and SO2. FATE supports 165 countries; an example of the sensitivity of USA PM2.5 exposure to NOx emissions is shown in Figure 1.
The national population-weighted PM2.5 annual average concentrations (i.e., exposures) are calculated using satellite-derived estimates of surface PM2.5 concentrations at the 0.1° × 0.1° scale applied as downscaling factors to the GEOS-Chem model’s PM2.5 concentrations at the 2° × 2.5° resolution. The GEOS-Chem adjoint is then run at the 2° × 2.5° resolution to calculate the emission response coefficients. Using the fine-scale concentrations of the satellite-derived products improves the estimation of population exposure without changing the overall modeled value of PM2.5 concentrations at the coarse scale. However, given that there are appreciable differences between GEOS-Chem simulated PM2.5 concentrations and those of the satellite-based product at the coarse scale, we also include an option to adjust (“rescale”) the PM2.5 concentrations to match those from the satellite-based product, as the latter has been calibrated against a large collection of available in-situ measurements for 2010. For some applications using the adjoint sensitivities to estimate concentrations for years far from 2010, it may be desired to adjust the calculations to remove the rescaling because the satellite-derived estimates would no longer be representative of pollutant exposures.
Figure 2. Countries with PM2.5 sensitivities. 165 countries are supported.
The adjoint sensitivities can be optionally scaled such that the PM2.5 health impacts are consistent with the most up-to-date health impact assessment at this time – the GBD 2019 study. With this scaling, FATE is set up such that running the model with ECLIPSE 2019 anthropogenic emissions (the default) results in exactly the country-specific PM2.5 exposures from the GBD 2019 study.
The adjoint values are computed at the coarse scale, but the user may wish to provide emission perturbations at the fine scale. Within the script, we provide a simple mapping of finely-scaled (0.1° × 0.1°) emissions to the coarse scale (2° × 2.5°).
O3
For O3, we directly use simulated surface O3 concentrations at the 2° × 2.5° resolution. Within the GEOS-Chem adjoint model, the exposures are computed as the maximum 6-month mean of the daily 1-hour maximum O3. Due to the non-linearity of O3 chemistry, the local linear response calculated by the adjoint will not be representative of actual changes in O3 exposure over large changes in emissions. To account for this, we include the option to scale adjoint sensitivities to anthropogenic exposures, calculated from GEOS-Chem, based on input anthropogenic emissions. This methodology is identical to what is done for PM2.5.
The unscaled adjoint sensitivities are the local linear response of a pollutant exposure to changes in emissions and are most applicable over small emission perturbations where the non-linear effects are smaller. The anthropogenic scaled sensitivities are most applicable over larger changes in emissions. We suggest that, if possible, users run scenarios using both the unscaled and scaled sensitivities. Following this, users can choose the more appropriate run and use the difference between the two runs as an uncertainty bound, on either side, to assess uncertainty in the exposure estimate. Rather than propagating this uncertainty into the health calculation, we suggest that users consider uncertainty from the exposure calculation as separate from the health calculation.
Figure 3. Countries with O3 sensitivities. 19 individual G20 countries and 24 additional EU member countries are supported.
O3 exposure is sensitive to volatile organic compounds (VOCs); however, there are only a few species of VOCs that are considered in GEOS-Chem. For more accurate VOC scenarios, we suggest that users only consider emissions of the following species: ≥C4-alkanes, formaldehyde (HCHO), ethane (C2H6), propane (C3H8), propene (C3H6), acetone, methyl ethyl ketone and acetaldehyde.
The O3 exposures calculated in GEOS-Chem differ from those used in the GBD 2019 study; the latter incorporate both in-situ monitor observations and simulated concentrations from multiple models using a kriging methodology. Consistent with the sensitivities for PM2.5, an additional scaling factor has been calculated to convert sensitivities from being with respect to the GEOS-Chem exposures (based on the maximum 6-month mean of the 1-hour daily maximum) to being with respect to the GBD 2019 study exposures (based on the 6-month mean of the 8-hour daily maximum).
Health impacts for O3 can also be assessed using different exposure estimate methods if desired. The O3 exposure sensitivities are calculated for a metric of the maximum 6-month mean of the daily 1-hour maximum O3 at the surface level (~50 meters), which is the approximate center altitude of the first layer of GEOS-Chem. Additionally, the maximum 6-month mean O3 has been calculated for the 8-hour daily max, and adjusted to a height of 2 meters (a level more consistent with O3 exposure), and the ratio of these two quantities are provided as scaling factors for each country. These ratios can be applied by the user (to the total exposure, adjoint coefficients, and natural exposure in each country) to estimate health impacts based on the maximum 6-month mean of daily 8-hour max concentrations at the 2m height, rather than the 6-month mean of daily 1-hour max at ~50 m.
Perturbing emissions
In FATE, the baseline emissions are derived from the ECLIPSE V5a Reference scenario, which provides gridded emissions data globally at a resolution of 0.1° × 0.1° for each precursor species and sector. The baseline ECLIPSE data in FATE covers multiple years, including 2015, 2020, 2030, 2040, and 2050, with intermediate years interpolated. Users can perturb these baseline emissions for specific sectors, precursor species, years, and countries.
A gridded emissions perturbation is element-wise multiplied by the ECLIPSE emissions for the corresponding sectors, species, and years at the 0.1° × 0.1° resolution. FATE then re-grids the perturbed emissions to the 2° × 2.5° grid and performs element-wise multiplication with the adjoint sensitivities to calculate population-weighted exposure to PM2.5 or O3. This population-weighted exposure is used in the impacts module to calculate the health burden associated with the perturbed emissions.
To perturb emissions for an entire country, users specify a tabular input as a CSV file containing the desired emissions perturbations for different sectors, species, and years. FATE distributes this perturbation over ECLIPSE’s 0.1° × 0.1° grid by filling cells corresponding to the specified ISO with the specified perturbation using the internal country mask. In cases where multiple countries occupy a single grid cell, FATE applies border weighting to reduce the perturbation according to the fraction of the grid cell area occupied by the specified country.
In place of inputting a perturbation for an entire country, users can specify a gridded perturbation as a netCDF file with a perturbation variable defined for sector, species, year, latitude, and longitude dimensions. This approach does not rely on FATE’s country mask and allows the user to specify perturbations outside of ISO land boundaries. Users can specify a gridded perturbation at the 0.1° × 0.1° resolution of ECLIPSE or the 2° × 2.5° resolution of the adjoint sensitivities. The gridded input option is particularly useful when emissions are not contained to national borders such as for maritime shipping and international aviation.
Users have three options for specifying how FATE should interpret the values of these perturbations: relative perturbation, absolute perturbation, and independent emissions.
Relative Perturbation
The relative perturbation option enables users to simulate the effects of percentage changes to emissions. This option is particularly useful for exploring the potential benefits from reductions in specific sectors, species, or regions, without requiring absolute emission reduction estimates. Inputs are provided as relative fractions with a value of one representing no change from the ECLIPSE baseline.
To apply a relative perturbation, FATE multiplies user-specified relative fractions by corresponding ECLIPSE emissions for the specified species, sectors, and years using the gridding methods outlined above.
Absolute Perturbation
The absolute perturbation option models change from FATE’s baseline as an absolute quantity, specified in units of tonnes, kt, or \(kg/m^{2}\). This perturbation type is useful when the baseline scenario does not accurately represent total-sector emissions or when the user wants to focus on specific segments of a sector.
To obtain the absolute perturbation input for FATE, the user subtracts their baseline scenario emissions from each alternate scenario for corresponding ISOs, species, sectors, and years. Positive absolute perturbations increase emissions compared to the baseline, while negative perturbations reduce baseline emissions.
For a tabular input, FATE calculates an equivalent relative perturbation with respect to the ECLIPSE baseline. This conversion is done by adding the absolute perturbation to corresponding ECLIPSE emissions for specified ISOs, species, sectors, and years and dividing by the same corresponding ECLIPSE emissions. The model then applies the same gridding process as for a relative perturbation. Converting to a relative perturbation ensures that the perturbation is distributed appropriately based on the magnitude of the unperturbed emissions.
In the case of a gridded absolute perturbation, the ECLIPSE baseline is directly perturbed for specified species, sectors, and grid cells by adding the gridded absolute perturbation to the baseline without the need for a conversion to a relative perturbation.
Independent Emissions
The independent option allows users to replace a portion of FATE’s baseline with their own emissions, measured in tonnes, kt, or \(kg/m^{2}\). This option is particularly useful when the user has confidence that their baseline case accurately represents total-sector emissions.
Similar to handling tabular absolute perturbations, tabular independent emissions are also converted to relative perturbations in FATE. This conversion involves simply dividing the independent emissions by FATE’s baseline emissions for specified ISOs, species, sectors, and years. The model then calculates gridded perturbed emissions and exposure using the same process as for relative and absolute cases.
For gridded independent emissions, the user’s input replaces the ECLIPSE baseline directly for specified species, sectors, and grid cells after necessary unit conversion or re-gridding.
Health impact assessment methods
The health impacts of PM2.5 and O3 exposure are calculated for each country using the “attributable fraction” approach. This approach is widely used by the GBD study, the World Health Organization, the U.S. Environmental Protection Agency, and throughout the peer-reviewed literature. For each scenario, FATE estimates the number of cases of various health endpoints by age group attributable to each pollutant.
Health impact methods are consistent with the GBD 2019 study, published in June 2020. GBD studies are broadly respected and increasingly used to inform public health decision-making around the world, at all geopolitical levels – international, national, and sub-national. Risk-outcome pairs are only included in the GBD after thorough review of the epidemiological, toxicology, and human and animal study evidence. The GBD is published annually and is updated over time to reflect the evolution of the state of the science, including in epidemiology and air pollution exposure science.
Consistent with the risk-outcome pairs in the GBD, FATE calculates cases of the following health outcomes associated with PM2.5:
-
stroke
-
ischemic heart disease
-
chronic obstructive pulmonary disease (COPD)
-
lower respiratory infection
-
lung cancer
-
diabetes mellitus type 2
For O3, only cases of COPD are considered.
The equation used to calculate the disease burden associated with PM2.5 and O3 concentrations is:
\[M_{a,i,h} = \text{Pop}_{i} \times \ \text{Popfrac}_{a,h} \times Y_{a,c,h} \times \left\lbrack \frac{\text{RR}_{a,i,h} - 1}{\text{RR}_{a,i,h}} \right\rbrack\]Where:
-
\(M\) is the disease burden (pollutant-attributable deaths or years of life lost) in geographic unit \(i\) for age group \(a\) and health endpoint \(h\)
-
\(\text{Pop}\) is the population in the geographic unit \(i\)
-
\(\text{Popfrac}\) is the population fraction for age group \(a\) and health endpoint \(h\)
-
\(Y\) is the baseline incidence rate (deaths or years of life lost per 100,000 people) in country \(c\) for age group \(a\) and health endpoint \(h\)
-
\(\text{RR}\) is relative risk in grid cell \(i\) for age group \(a\) and health endpoint \(h\)
The quantity in brackets is the population attributable fraction – the fraction of disease in a population that is attributable to the risk factor (in this case annual average PM2.5 or six-month average of 8-hour daily maximum O3).
A key feature of the PM2.5 concentration-response curves is that they are nonlinear and flatten considerably at high concentrations, particularly for cardiovascular health endpoints. The shape of the concentration-response curve implies that sensitivity of health effects to a unit change in PM2.5 concentration in very polluted environments is diminished compared to that in clean environments. Therefore, rather than using a continuous parametric function, we use RR lookup tables, which are provided by the GBD 2019. RRs between concentration points in the lookup tables are linearly interpolated.
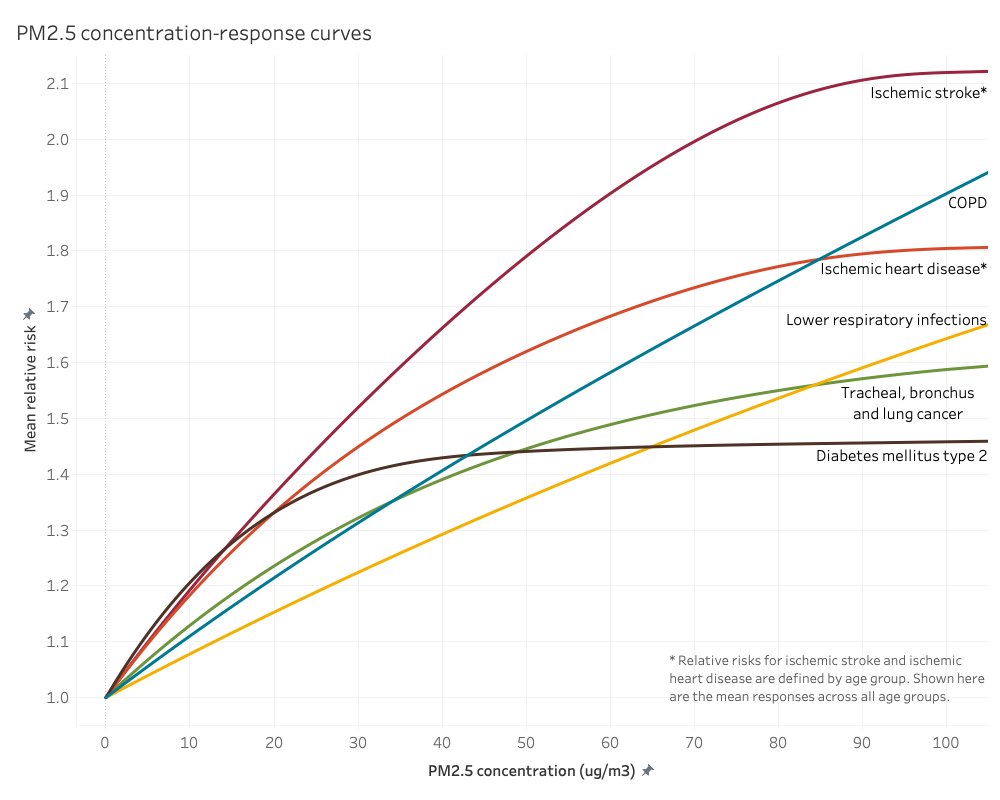
Figure 4. PM2.5 concentration-response curves for each health endpoint. Ischemic stroke and heart disease have different curves for each age group, however just the mean response is shown here.
For O3, the same RR estimate is used at all concentrations: 1.06 (95% CI 1.03, 1.10) per 10 ppb O3 increase (six-month average of the 8-hour daily maximum). This RR is based on five studies of long-term O3 exposure and COPD from Canada, the United Kingdom, and the United States. We assume the concentration-response curve for O3 is log-linear (the natural log of RR is linearly associated with O3 concentration). With this assumption, a RR of 1.06 translates to a concentration-response factor of 0.005827 (calculated by \(\ln{(\frac{\text{RR}}{10})}\)). This assumption is also used by the GBD and throughout the scientific literature.
The GBD 2019 study calculates the health burden from O3 exposure above a theoretical minimum risk exposure level (TMREL) taken from a uniform distribution between 29.1 – 35.7 ppb. We cut off any calculation of risk below the midpoint of this range, 32.4 ppb. We have decided not to use a TMREL for PM2.5 as use of the model typically focuses on smaller perturbations in concentrations well above the TMREL. In addition, epidemiological studies are finding PM2.5 mortality effects at lower and lower concentrations, down to approximately 2 µg/m3, so calculating health impacts at very low concentrations is justified by the current evidence. The TMREL is more important for O3, however, because it’s a larger fraction of the total concentration.
Future baseline disease rates
GBD 2019 gives annual baseline disease rates up to 2019, however a key feature of FATE is estimating the impacts of exposure changes into the future. In order to determine a baseline for projected disease rates we refer to the GBD Foresight project. We use their values through 2040, extending the 2040 rates forward for any years beyond. The dataset of future disease rates for each of the causes affected by air pollution was created by Rita Van Dingenen from Joint Research Centre of the European Commission. As the GBD Foresight projections were based on the GBD 2015 study, Van Dingenen scaled the original GBD Foresight future rates by the ratio of GBD 2017 to GBD 2015 values for the year 2015. Rates for diabetes mellitus type 2 are held constant at present-day levels since the Foresight project only provided future rates for type 1 and type 2 diabetes together.
Scaling was performed for each cause, land, age group:
\[\text{GBDForesight}_{\text{Scaled}(\text{Year})} = \text{GBDForesight}_{\text{Download}(\text{Year})} \times \ \frac{ {\text{GBD}2017}_{2015}}{\text{GBDForesight}_{\text{Download}(2015)}}\]We then performed further rescaling to be consistent with the GBD 2019 to avoid a substantial disconnect between historical and projected baseline rates. To rescale to the 2019 values, we first calculated the annualized percent change in Van Dingenen’s estimates from 2015-2020, 2020-2025, and so on until 2040. Then we matched these to the corresponding country-cause-age combination in the GBD 2019 data for 2019. We applied the 2015-2020 annualized rate for one year to calculate 2020 projected values from the 2019 data, then we applied the other rates to calculate annual projections to 2040.
Vsl calculation
The value of statistical life (VSL) is an economic concept that quantifies the economic value nations place on reducing the risk of premature death. It represents the monetary value that society is willing to pay to prevent a statistical average loss of life. VSL is an important tool used in cost-benefit analysis, particularly in evaluating public health and environmental regulations. The value assigned to a statistical life can vary across countries, regions, and contexts due to differences in societal values, income levels, and other cultural and economic factors.
In FATE, the calculation of VSL is an optional feature that can be performed alongside the estimation of health burden. The model takes into account the influence of a nation’s wealth on its ability to allocate resources for reducing the risk of premature death and incorporates monetary inflation over time. It is important to note that the VSL calculation in FATE focuses solely on the avoidance of premature death and does not include the added value of preventing disability.
FATE utilizes two distinct methods for the calculation of VSL to quantify the number of premature deaths by country, age, and causes. These methods are from Viscusi and Masterman (2017), referred to as the “Viscusi” method in the model, and from Narain and Sall (2016), referred to as the “World Bank” method because the World Bank published this report. Both methods involve multiplying the baseline VSL for a nation in a given year by the number of premature deaths generated by FATE’s health impacts module. However, the two methods yield different estimates due to variations in how the baseline VSL is calculated in each method.
Viscusi Method
To address the challenges of estimating VSL in different countries, Viscusi and Masterman (2017) propose a benefit transfer method that adjusts a base VSL for the United States (\(\text{VS}L_{\text{USA}}\)) of 9.6 million in 2015 USD by the relative incomes of the United States and the countries of interest.
FATE first modifies this value for baseline USA VSL into 2020 USD using the Bureau of Labor Statistics inflation rate calculator, which gives a value for an inflation factor, \(i_{2020}\), to convert from 2015 to 2020 USD. The inflation-adjusted value is further scaled to determine VSL for different countries in certain years. This scaling process involves multiplying the adjusted VSL value by the ratio of Gross National Income Per Capital, Atlas Method (GNI) of a specific country in 2015 to that of the United States. This ratio is raised to an income elasticity value, \(e\). The Viscusi method assumes that the income elasticity value is one. This assumption is based on an analysis by the authors on income data from various countries that revealed similarity in the income-to-VSL relationship compared to that of the United States, thus negating the need to raise the ratio of GNI Atlas to an exponent other than one. Further scaling by the growth rate in GNI Atlas of the country between 2015 and 2020 (\(g_{1}\)) yields the VSL in 2020 for a given country.
\[\text{VSL}_{ISO,\ 2020} = VSL_{\text{USA}} \times i_{2020} \times \left( \frac{\text{GNI}_{ISO,2015}}{\text{GNI}_{USA,2015}} \right)^{e} \times \left( 1 + g_{1,\ ISO} \right)\]The growth rate in the GNI Atlas for a specific country from 2015 to 2020, \(g_{1,\ ISO}\), is calculated as:
\[g_{1,ISO} = \frac{\text{GN}I_{2020,ISO} - GNI_{2015,ISO}{\times i}_{2020}}{\text{GN}I_{2015,ISO} \times i_{2020}}\]GNI Atlas data for most countries is collected from World Bank, with the exception of Taiwan, where national statistical data is used.
To adjust the ISO-specific VSL values from 2020 to another year, denoted \(t\), an additional growth factor, \(g_{t}\), is applied:
\[\text{VS}L_{ISO,\ t} = \text{VSL}_{ISO,\ 2020} \times (1 + g_{t,ISO})\]This adjustment considers the GNI Atlas data for a specific country in 2020, the GNI Atlas for the same country in year \(t\) and an inflation factor, \(i_{t}\), for converting from USD in 2020 to USD in year \(t\):
\[g_{t,ISO} = \frac{\text{GN}I_{t,ISO} - GNI_{2020,ISO} \times i_{t}}{\text{GN}I_{2020,ISO} \times i_{t}}\]In the Viscusi method, differences in baseline VSL for nations consider only the impact of direct currency conversion without the impact of national differences in purchasing power.
This estimate for a nation’s baseline VSL each year is multiplied by the number of premature deaths for each age category and cause, yielding total VSL from premature death by country, age, and cause.
World Bank Method
The World Bank method, based on Narain and Sall (2016), follows a similar mathematical approach as the Viscusi method but incorporates modified assumptions.
First, the base VSL value is set at 3.83 million, calculated as a World Bank average for 2011 in 2011 USD. Like the Viscusi method, the base VSL value is adjusted to 2020 USD using an inflation factor, \(i_{2020}\), from the Bureau of Labor Statistics inflation rate calculator that converts from 2011 USD to 2020 USD.
Instead of using a ratio of Gross National Income, the World Bank method utilizes a ratio of Gross Domestic Product per Capita, Purchasing Power Parity (GDP PPP) to scale the base VSL. The scaling factor is the ratio of a country’s GDP PPP in 2011 to a base GDP PPP of 37,350 for 2011 in 2011 USD, obtained from the World Bank. This scaling factor is raised to the income elasticity value, \(e\), which varies based on the income status of a country. If a country’s Gross National Income Purchasing Power Parity (GNI PPP) in 2011 exceeds 12,476 2011 USD, it is considered a high-income country, and the income elasticity is set to 0.8. For countries that do not meet the high-income threshold, the income elasticity is set to 1.2. GDP PPP and GNI PPP data are collected from the World Bank with the exception of data for Taiwan, which comes from national statistical data from the same source as in the Viscusi method.
To calculate the VSL value for a specific country in 2020, the inflation adjusted VSL value is multiplied by the income elasticity-adjusted ratio of the country’s GDP PPP in 2011 to the base GDP PPP set by the World Bank, and then multiplied by the growth rate of the country’s GDP PPP between 2011 and 2020, \(g_{1,\ ISO}\) plus one:
\[\text{VSL}_{ISO,\ 2020} = VSL_{\text{WB}} \times i_{2020} \times \left( \frac{\text{GDP PPP}_{ISO,2011}}{\text{GDP PPP}_{WB,2011}} \right)^{e} \times \left( 1 + g_{1,\ ISO} \right)\]The growth rate in the GDP PPP from 2011 to 2020 is calculated as:
\[g_{1,ISO} = \frac{\text{GDP PPP}_{2020,ISO} - \text{GDP PPP}_{2011,ISO} \times i_{2020}}{\text{GDP PPP}_{2011,ISO} \times i_{2020}}\]Subsequently, ISO-specific VSL values in other years, \(t\), for the World Bank method are determined by multiplying the VSL value in 2020 by a growth rate \(g_{t,ISO}\) of the country’s GDP PPP between 2020 and the year \(t\) as follows:
\[\text{VS}L_{ISO,\ t} = \text{VSL}_{ISO,\ 2020} \times (1 + g_{t,ISO})\]The growth rate takes into account the GDP PPP data for the specific country in 2020, the projected GDP PPP for the same country in year \(t\), and the inflation factor, \(i_{t}\), from 2020 to year \(t\):
\[g_{t,ISO} = \frac{\text{GDP PPP}_{t,ISO} - \text{GDP PPP}_{2020,ISO} \times i_{t}}{\text{GDP PPP}_{2020,ISO} \times i_{t}}\]Long-term income projections for a subset of countries come from a 2018 Organization for Economic Co-operation and Development (OECD) study for the years 2010, 2030, 2040, and 2050. Projections for the remaining countries are calculated based on Shared Socioeconomic Pathways 2 (SSP2) projections. If necessary, values are interpolated for intermediate years with growth rates adjustments.
These VSL estimates for each country in each year are then multiplied by the premature deaths generated by FATE’s health impacts module to determine associated welfare loss from premature death for each country, age category, and cause.